Aligned Structured Sparsity Learning for Efficient Image Super-Resolution
2021/12/14
来源:NIPS2021 - spotlight
resource:github上备份的包括ipad标注的pdf版本。
作者是张宇伦他们,Yulun Zhang, Huan Wang, Can Qin, Yun Fu。
Summary:一篇中规中矩的A+B文章。作者提出将pruning作为SR轻量化的方法(ASSL,regularization-based filter pruning method),做了些适应性变更。文章最突出的贡献是提出了一种基于gram Matrix的正则项约束残差块最后一层的剪枝通道一致,其次针对SR模型没有BN、无法确定重要性系数的问题,提出一种WN来归一并加权不同通道,并对这些系数用L2正则来实现稀疏化。
Rating: 3.0/5.0 一般,中规中矩
Comprehension: 4.0/5.0 比较容易理解
motivation:SR领域已有轻量架构设计与NAS、KD相关的方法,但是还没有人从pruning这个角度、从Conv通道冗余性的维度来讲故事。
文章的贡献有:
- 第一个做Pruning+SR的
- 提出一种regularization term来统一不同residual block最后的剪枝通道;
- 设计WN层,对归一化后的不同层乘以不同的系数,并对系数实现稀疏约束。
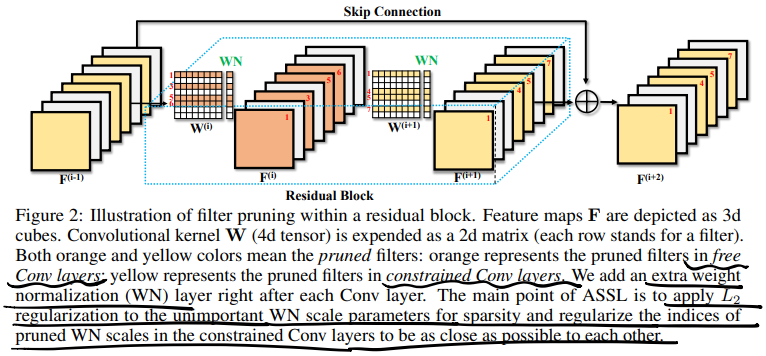
一张图总结全文:
1 Introduction
motivation(其实就是给自己A+B找个借口)简单介绍了Lightweight SR与SR + eff method(NAS、KD)的工作,指出他们没有从Conv kernel稀疏性的角度改善模型高效性,同时直接A+B比较困难(现在的SR模型里residual connections太多,但是残差块难剪,立意不强)。
2 Related Work
有点奇妙,学到了pruning相关的一些知识:可以分成regularization-based和importance-based两类范式,但是这两类之间没有严格的界限 这真不是你们自己侃出来的吗
3 Proposed Method
3.1 Deep CNN for Image SR
有一点preliminary(虽然很直观),HR图像的降采样过程会引入一些额外的噪声、模糊、压缩以及其他尚未明确的效应,同时高频部分也会损失。
3.2 Aligned Structural Sparsity Learning (ASSL)
讲得很清楚,分成了四个部分:
- 参数如何被归一化以获得稀疏性(what parameters are regularized to obtain sparsity -> Regularizing Scales in Weight Normalization);
- 如何选择并约束不重要的参数(how to select unimportant parameters to regularize -> Pruning Scheme and Criterion);
- 约束项的形式是怎样的(which is the specific regularization form -> Regularization Form);
- 如何对齐残差网络的稀疏结构(how to align the sparsity structure for residual networks -> Sparsity Structure Alignment)。
Regularizing Scales in Weight Normalization -> WN
分类任务有BN,可以直接把BN中的scaling factor作为不同通道重要性的约束gate变量,但是SR里不含BN(BN对SR任务有害),为了获得这样的gate scale factor,作者提出在每层后面附上一个weight normalization层,将层中的参数归一化并乘以可学习的scale parameter:
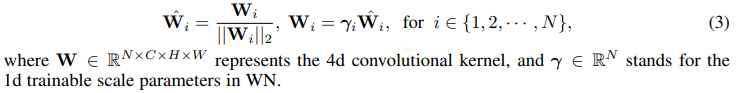
Pruning Scheme and Criterion -> L1-norm、local pruning
作者称分类任务里globally排列BN scale,但是在SR任务里这么做不行,因为难以保证相加的两层通道数一致,因此他们采取了局部剪枝的策略,即在一层内达到剪枝比率,使用的剪枝标准是L1-norm。具体的流程是,对于第l层,将通道按照L1-norm排列,将最不重要(L1-norm最低)的通道选出来作为一个集合$S^({l)}$,对这些不重要的通道施加sparsity-inducing regularization(重要的通道不做任何处理)。
Regularization Form -> L_{SI}
将WN系数的L2-norm作为sparsity-inducing regularization,具体形式为:
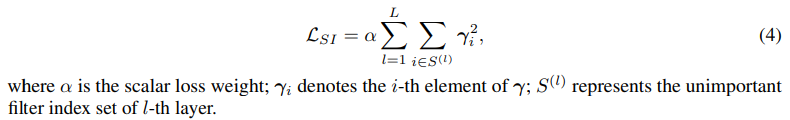
其中加权系数\alpha随着训练进行逐渐增大,达到一个上界\tao的时候剪枝结束。
Sparsity Structure Alignment
作者将网络中的层分成了两个部分,见第一张图,残差块中的第一层是可以随便剪的层(free Conv layers),第二层因为shortcut的存在不能随便剪(constrained Conv layers),需要对这些受限的层额外施加一些限制。
- 这里还对比了图像分类任务,但是我觉得有点牵强,
而且只字未提一样的硬Mask:- SR任务比分类任务更深,有更多residual block;
- SR使用两层的残差块,分类任务用bottleneck,SR任务里constrained Conv layers占比高;
- 分类任务残差块最后一层是1*1 Conv,就算不剪枝FLOPs也少,但是SR残差块第二层就是普通尺寸Conv。
具体做法是用mask的内积作为约束项:
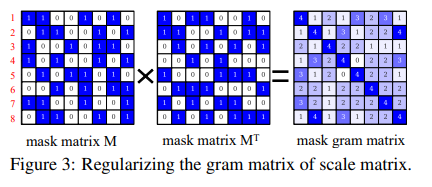
L_{SSA}的具体形式为:
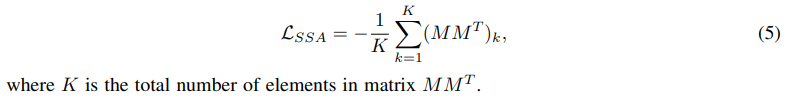
考虑到上面的硬mask不可微,他们用WN系数的sigmoid值作为软mask,填到上面的term里:
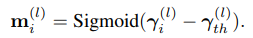
所以他们从头到尾没有施加硬约束,就靠这个软性term限制剪枝通道,最后也没放剪枝后的通道分布。
3.3 Arm Image SR Models with ASSL
剪枝pipeline:
- 对于free Conv layers直接施加SI regularization;
- 对于constrained Conv layers先施加sparsity-structure alignment regularization训上若干epoch,再上SI regularization;
- 剪枝结束后移除剪枝掉的通道和WN层。

4 Experimental Results
- 数据集:
- 训练集是DIV2K和Flickr2K
- 测试集是Set5,Set14,B100,Urban100,Manga109
- SR的常用设置,在YCbCr空间的Y通道上测PSNR和SSIM
- 训练设置:
- 训练数据aug,0°/90°/180°/270°旋转与垂直翻转;
- bs=16, patch size=48*48
- Adam optimizer,lr 1e-4 -> 1e-5
- 实验结果:
-
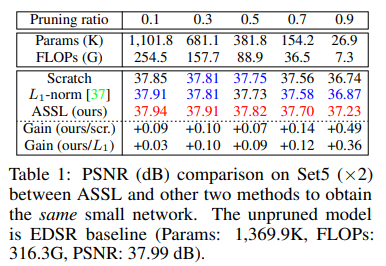
Ablation 1 - 和navie L1-norm / train from scratch比:
-
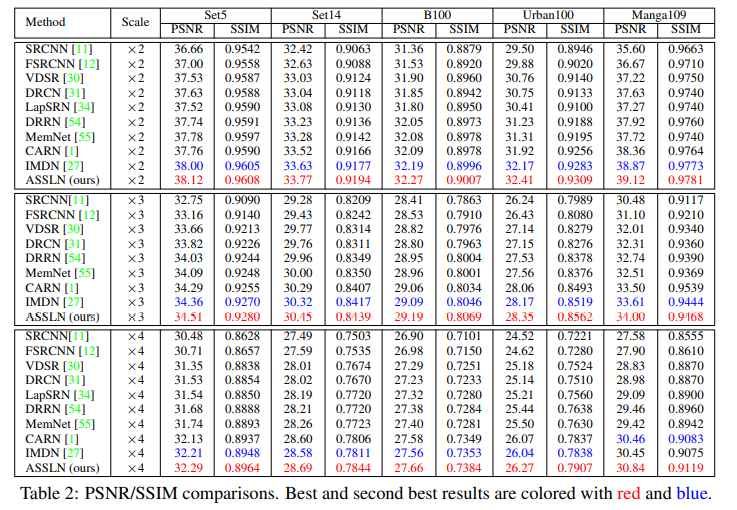
Main Result 1 - 主要和LightWeight SR模型比:
-
Main Result 2 - 比模型size和MAC:
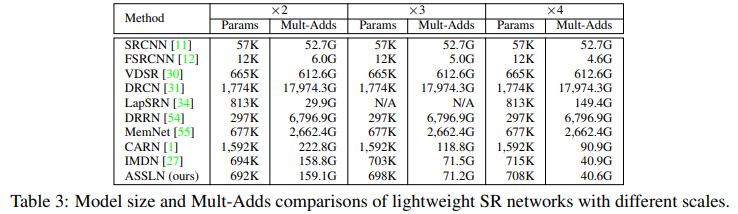
-
Ablation 2 - 和其他轻量算法(NAS / KD)比:
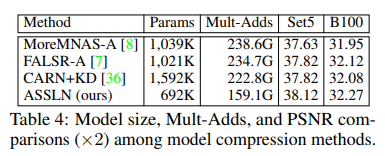
-