Brief review of image denoising techniques

2021/9/3

来源：一个线上期刊，感觉不是很好 - Visual Computing for Industry, Biomedicine, and Art 19
resource：github上备份的包括ipad标注的pdf版本。
作者是山大的Linwei Fan。

Summary：水平比较差的一篇综述，前面的传统方法总结得甚至不如印度人细，后面的NN-based方法实在太烂。

rating：0.9/5.0
comprehension：3.0/5.0(传统方法不太理解，不知道水平几何)

Introduction

  • 噪声、边缘和纹理都是高频成分，在去噪的时候很难区分这三者，因此会不可避免地损失细节。
  • 从数学的角度而言去噪是个inverse / ill-posed problem，没有唯一解。
  • 去噪问题的定义还挺清楚的：The purpose of noise reduction is to decrease the noise in natural images while minimizing the loss of original features and improving the signal-to-noise ratio (SNR).
  • 去噪问题的挑战主要有：
    • 平坦区域(flat areas)应该平滑；
    • 边缘(edges)不能被模糊；
    • 纹理(texture)应该被保护；
    • 不能引入新的伪影(artifacts)。

Denoising Methods

甚至没能跳出这张图总结的范围（甚至不如三哥的总结）：

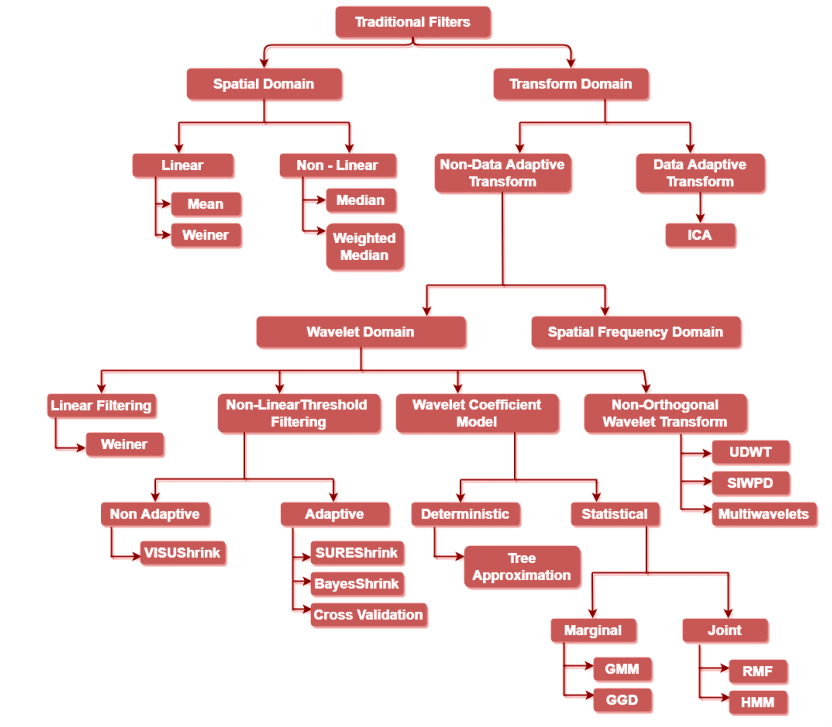
传统方法的分类为：

  • Spatial Domain Methods
    其定义为Spatial domain methods aim to remove noise by calculating the gray value of each pixel based on the correlation between pixels/image patches in the original image，也就是用像素/图像块之间的空间依赖关系计算合适的像素值进行去噪。
    • Spatial domain filtering
      空间滤波器方法建立在噪声占据了频谱中的高频部分，使用低通滤波器可以去除噪声的理论基础上。
      • Linear Filters：可以在空间域去除噪声，但是很难保存纹理。e.g. Mean Filtering, Wiener Filtering.
      • Non-linear Filters：e.g. Median Filtering, Weighted Median Filtering, Bilateral Filtering.
    • Variational denoising methods（这块还挺难的）
      变分去噪方法使用图像先验，通过最小化能量函数E来计算去噪后的图像，其动机是MAP：

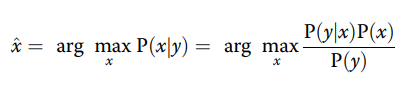
      可以被等效地表示为：

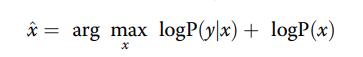
      在AWGN的情形下，目标函数可以表示为：

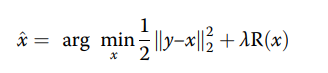
      第一项表示原始图像和噪声图像之间的差距，被称为data fidelity项；第二项是正则项，变分去噪问题的关键就是找到合适的图像先验（第二项）
      • Total variation regularization
        基于统计特性 - 自然图像局部光滑，像素值在大多数区域逐渐变化。可以保留sharp edge但是有三个缺点：1)over-smoothed texture, 2)flat areas are approximated by a piecewise constant surface resulting in a stair-casing effect, 3)losses of contrast
      • Non-local regularization
        局部去噪时间复杂度低但是噪声等级高了之后效果就差，这是因为高等级的噪声会干扰临近像素之间的关系。e.g. NLM(non-local means), NSS(non-local self-similarity),WNNM(weighted nuclear norm minimization)
      • Sparse representation
        每个图像patch都可以表示为over-complete dictionary中patch的线性组合。去噪的过程就是重建这个过程？可以灵活反应图像结构，缺点是忽略了图像的非局部关联。e.g. K-singular value decomposition (K-SVD) algorithm, NCSR(non-local centralized sparse representation, NSS+sparsity)
      • Low-rank minimization
        将相似的patch建模为matrix，Each column of this matrix is a stretched patch vector. By exploiting the low-rank prior of the matrix, this model can effectively reduce the noise in an image，可以进一步分成
        • low rank matrix factorization 低秩矩阵分解就用两个小矩阵的乘积近似大矩阵。相似的patch被低秩分解以去除噪声。这类方法的缺点是必须将秩作为输入，太小的秩会损失细节，太高会保留噪声。
        • NNM(nuclear norm minimization)
          methods based on NNM aim to find the lowest rank approximation X of an observed matrix Y，NNM中参数的singular value都一样，改进的方法是WNNM(和上面有关系？又是A+B？)这类方法的缺点是计算开销大。
  • Transform Domain Methods
    变换域方法基于这样的观察：图像信息和噪声在变换域中的表现不同。根据变换基选择的不同，可以进一分成：
    • Transform domain filtering methods
      • Data adaptive transform
        e.g. ICA(Independent component analysis，适合去噪非高斯噪声), PCA
        共同的缺点是计算代价高，因为需要采样没有噪声的数据because they use sliding windows and require a sample of noise-free data or at least two image frames from the same scene
      • Non-data adaptive transform
        • spatial-frequency domain
          像Fourier transform这样的，这种方法耗时较多，且取决于截断频率和filter的表现。
        • wavelet domain
          具有多尺度和稀疏性的特点。非常依赖小波基的选取，选取不当去噪效果就很差，所以是不具数据适应性的方法。
          • Linear
          • Non-linear
    • BM3D
      在变换域进行两次非局部协同滤波的方法。步骤是：
      1. 相似的patch通过block matching堆叠成3D group；
      2. 3D group转换到小波域；
      3. 进行hard thresholding或者Wiener filtering；
      4. 根据系数进行逆变换(inverse transform)。
        但是噪声等级逐渐增加BM3D的性能会下降很厉害，并引入伪影，尤其是在平坦区域。

Metrics of denoising performance & Conclusion

  • 目前没有明确的数学方法来评价感官质量，感官质量主要取决于三方面：
    • significant degree of artifacts
    • protection of edges
    • reservation of textures
  • 结论里强调现在绝大多数的方法都致力于去除AWGN噪声，只有很少一部分考虑真实图像去噪（因为真实图像太难而且缺乏训练的成对图像）。