Differentiable Soft Quantization: Bridging Full-Precision and Low-Bit Neural Networks
2021/9/5
来源:ICCV19
resource:github上备份的包括ipad标注的pdf版本。
作者是北航刘祥龙组,一作龚睿昊,tql。其余作者有Shenghu Jiang, Tianxiang Li, Peng Hu, Jiazhen Lin, Fengwei Yu, Junjie Yan。
Summary:模型量化领域一篇比较经典的文章?做的是在训练过程中逐渐改变sign函数的形状,在forward阶段减少量化误差,在backward阶段减少梯度误差。文中只是argue自己可以减少前向中的量化误差,并没有数据支撑,感觉本质上还是对STE的修改?他们的方法只是在forward阶段由quantize-dequantize改成了DSQ-quantize-dequantize,还是需要硬量化这个操作的。不过据MQBench说DSQ的提升只有20%是算法改进,80%的提升是训练的改进?(笑
文章贡献:
- (属于一种即插即用的module)用一系列超参数(差距值\alpha,截断上下限l和u)控制sign函数的形状,在训练中逐渐模拟staircase
Rating: 3.8/5.0
Comprehension: 4.5/5.0
一张图总结全文环节:
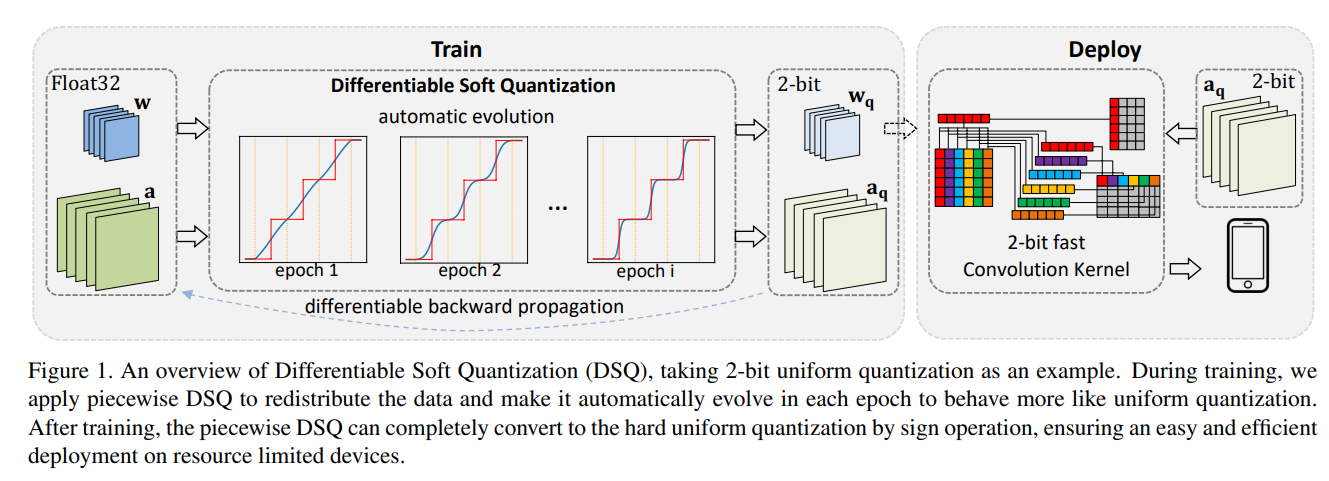
1 Introduction
- 受到指令集等硬件特征的限制,大多数量化方法很难实现硬件加速,很大程度上依赖特定硬件的设计和长期硬件开发。
- 研究表明binary和均匀量化是硬件友好型的。
- 一般量化方法的缺点主要表现在forward阶段的量化误差和backward阶段的STE(尤其是极低比特的情形,放大了量化的影响)。
- forward阶段的量化误差表现为rounding误差和clipping误差,两者相互掩护:量化器截断多些的话截断误差就大,rounding误差就小,verse versa
2 Related Work
这里面对量化方法的罗列还挺好的:
- bit operation
- x-bit uniform fix-point quantization
- 找每层的最佳比特位宽
- 增量(incremental)渐进(progressive)量化
- 网络结构
- KD
3 Differentiable Soft Quantization
3.2. Quantization function
这里给出了他们定义DSQ的函数形式,首先是每个分段的函数:
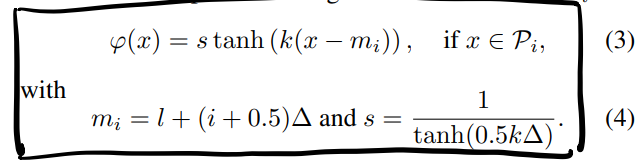
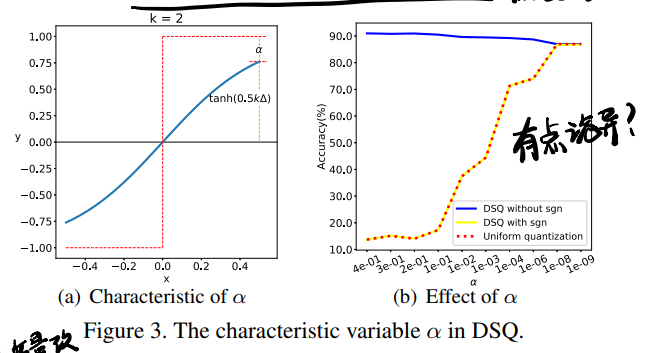
\phi就是每段的函数,s作为scale factor保证了每段函数之间的连续性,k则是用来逼近sgn的变量,这个值越大就越接近阶梯函数。后面引入了一个特性变量(如下图所示,衡量DSQ上限和+1的区别)来描述s与k,使得DSQ变成关于\alpha和△的函数:
s可以改写为:
\[s=\frac{1}{1-\alpha}\]k可以改写为:
\[k=\frac{1}{\vartriangle}log(\frac{2}{\alpha}-1)\]最后DSQ整体表示为:
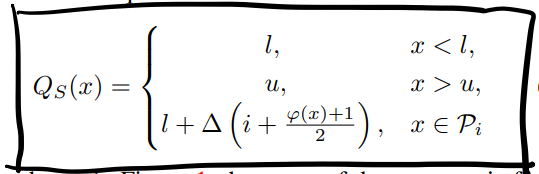
这里作者argue DSQ可以视为一种rectifier,可以让数据重新分布来减少量化点和量化值之间的距离。
3.3. Evolution to the standard quantization
这里把\alpha、clipping上界u和下界l当成优化变量就实现了学习过程中的进化。说是按层的loss,但是没给具体形式(大约也不用给):

3.4. Balancing clipping error and rounding error
通过联合优化u和l实现,u和l的偏导就是对DSQ的直接求导,挺简单的:
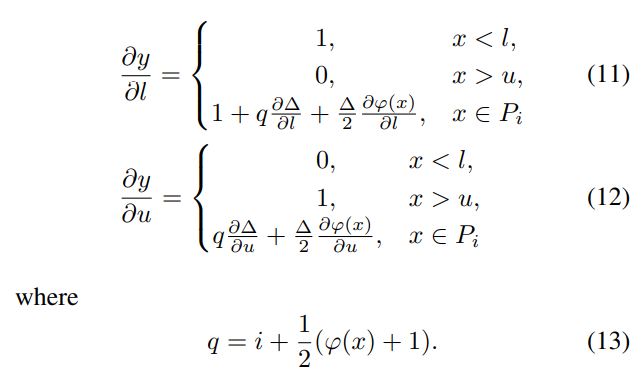
根据上式,大的outlier被u截断,主要贡献于u的更新;小的outlier被l截断,对l的更新做贡献;l和u之间的数据点则同时影响u和l的更新。当clipping error占主导时outlier的梯度很大,成为参数更新的主要动力;当rounding error占主导时,范围内的数据的梯度则更加重要,这样就自动实现了clipping error和rounding error的平衡。
3.5. Training and Deploying
算法流程图,重要的点用笔标出来了:

后面的硬件部分过于困难,无法理解。
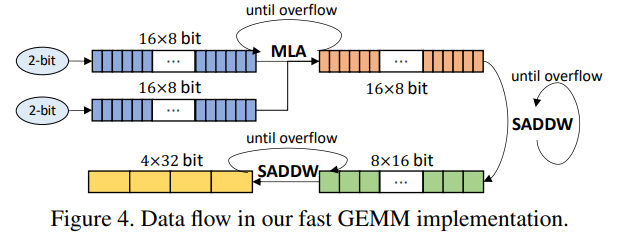
4. Experiments
- DSQ的桥梁作用:
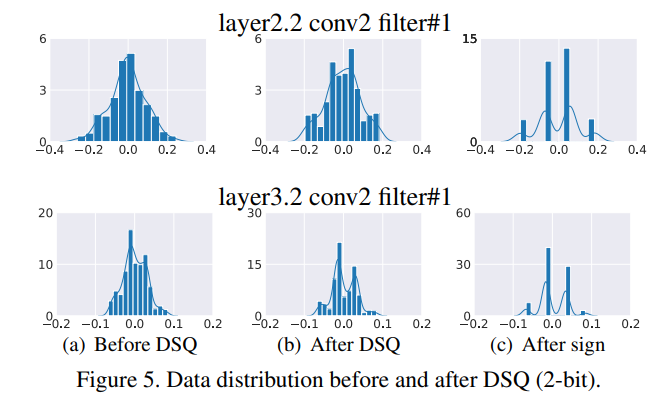
- 和之前工作结论的关联:
- alpha一开始设置为0.2,在训练的早中期会变成接近0.5的值,说明训练早期不要量化太多
- 参数的alpha比激活值的要小,说明参数对量化的容忍程度更高
- 不同层对量化的敏感度不同,这里说降采样层可以量化更多??
- 更低的比特不代表更快的推理速度,这主要是由于overflow和寄存器之间的数据转移造成的。