2021/5/19结果反馈与讨论记录
2021/5/15
BinaryDuo设置实验后续
搜索超参(epsilon for CDG & sigma for NES) - 1
实验设置:
- 沿用BinaryDuo上实验设置(2 models / gaussian data);
- 没有预训练,简单检查超参对CDG/NES的影响。
困难:
-
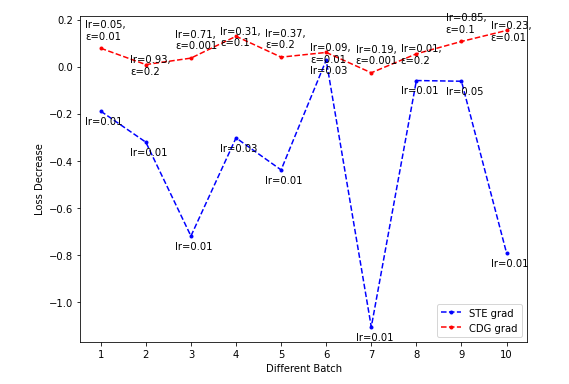
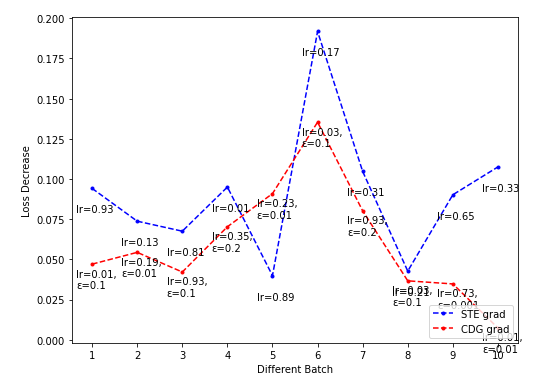
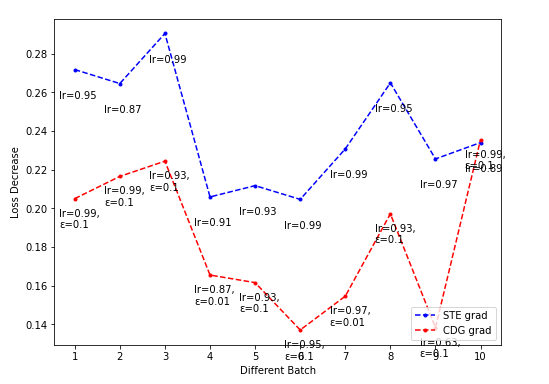
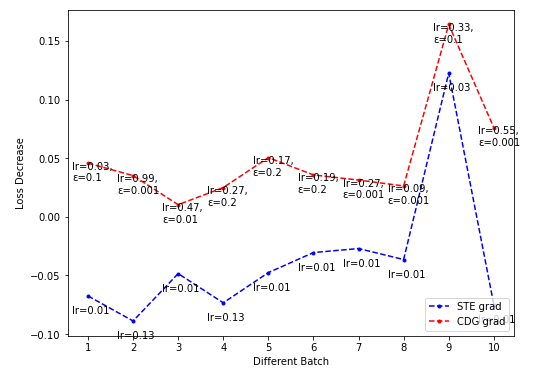
NES的超参sigma搜索起来代价太大(花费时间太长),而CDG的超参epsilon在Toy model上搜索较快,可饱和搜索,因此希望CDG的表现持续弱于某一NES的表现(这样就不用搜索NES超参的最佳值了)。
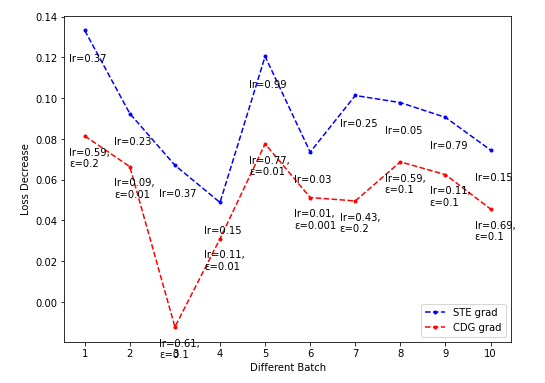
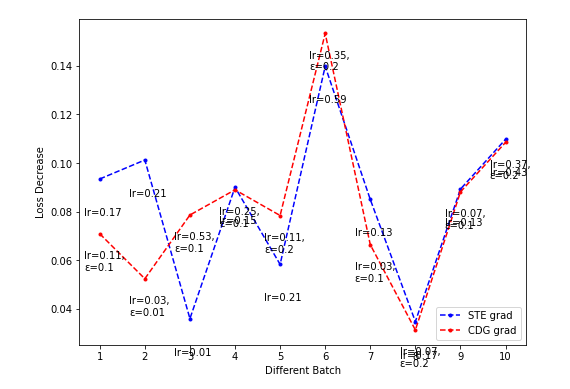
- CDG lr-loss decrease plot
-
Dim = 8
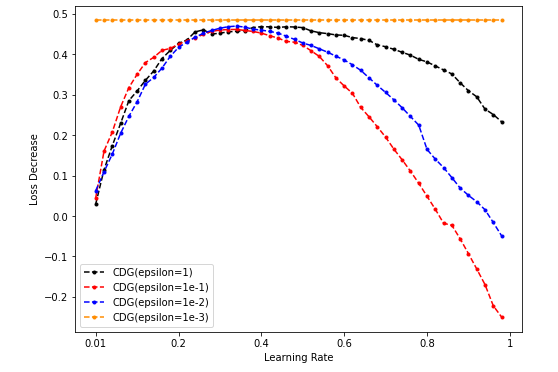
-
Dim = 16
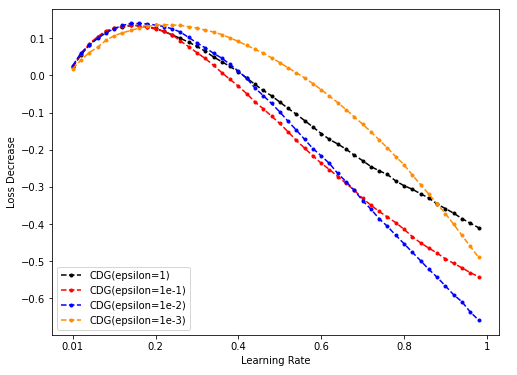
-
Dim = 32
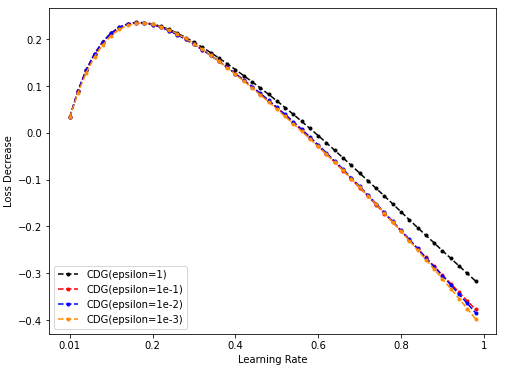
-
Dim = 64
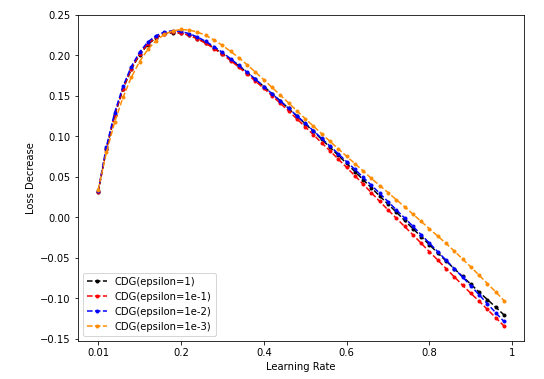
-
- NES lr-loss decrease plot
-
Dim = 8 Sample = 500
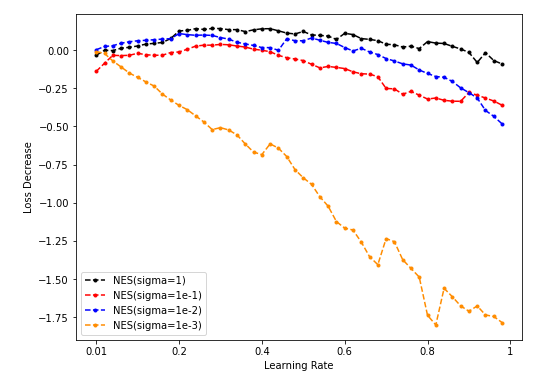
Sample = 5000
Sample = 50000
-
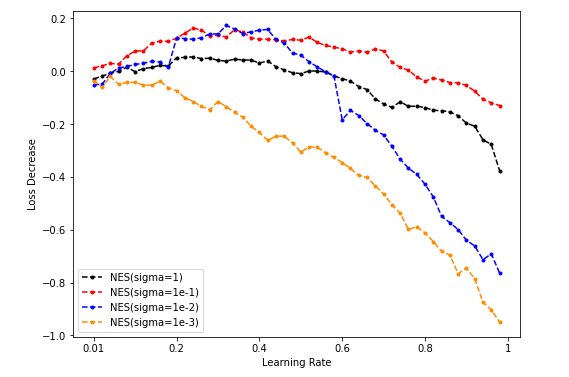
Dim = 16
Sample = 500
Sample = 5000
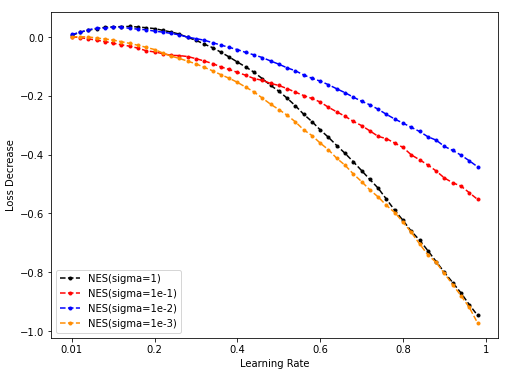
Sample = 50000
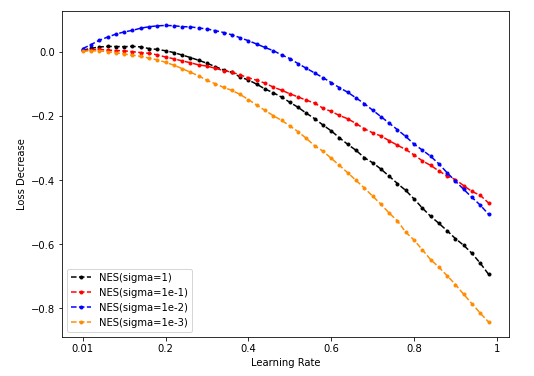
-
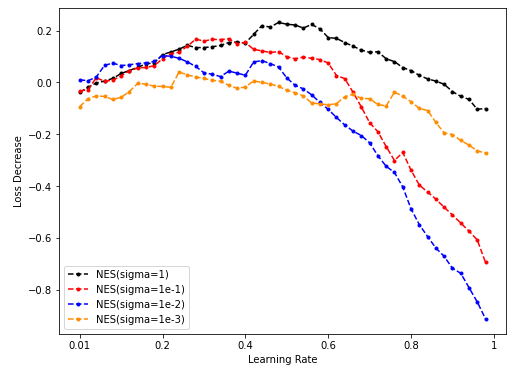
Dim = 32
Sample = 500
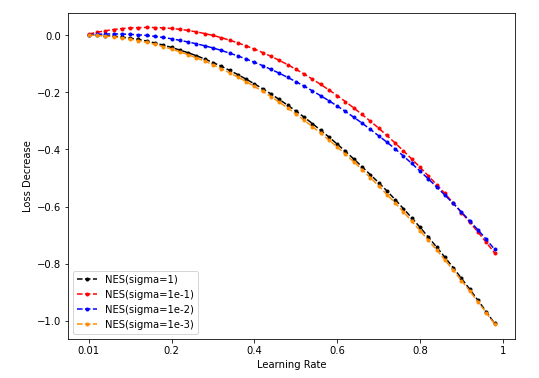
Sample = 5000
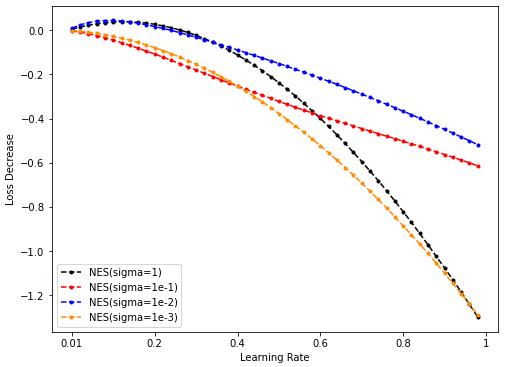
Sample = 50000
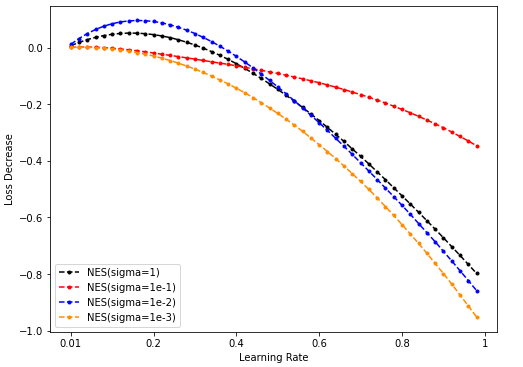
-
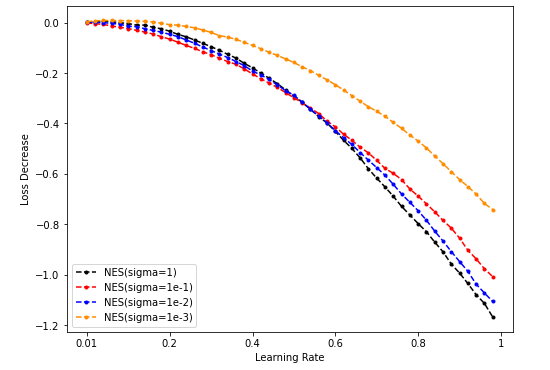
Dim = 64
Sample = 500
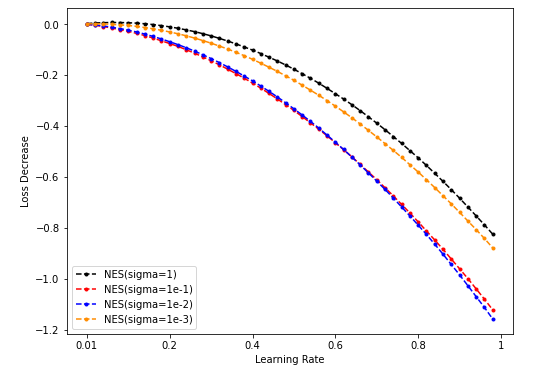
Sample = 5000
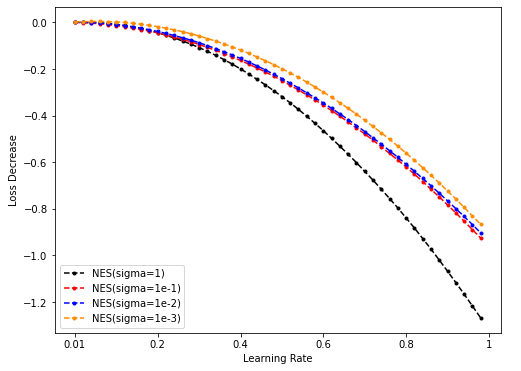
Sample = 50000
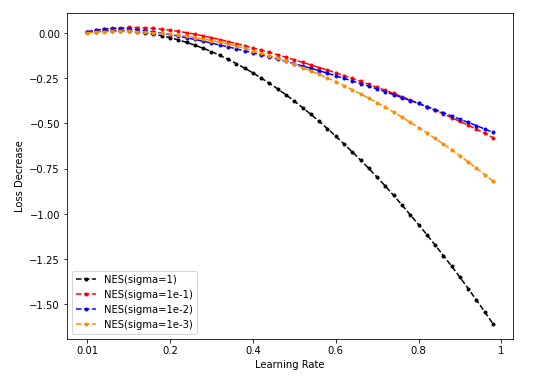
-
- best loss decrease - num_dim plot
搜索超参(epsilon for CDG & sigma for NES) - 2
实验设置:
- 沿用BinaryDuo上实验设置(2 models / gaussian data);
- 进行了预训练,使用2000个(16000, num_dim)~N(0, 1)的数据将evaluate_model训练到基本收敛(loss不再出现明显下降)。
问题:
NES grad似乎不能指向loss下降的方向
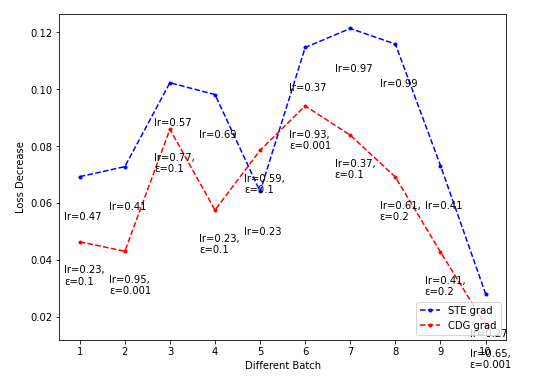
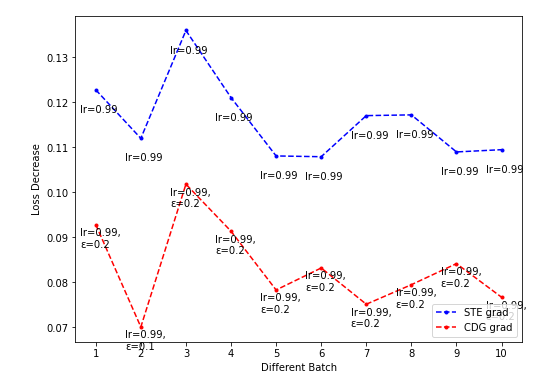
- CDG lr-loss decrease plot
-
Dim = 8
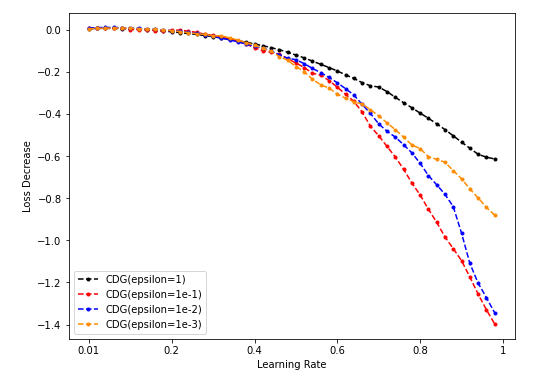
-
Dim = 16
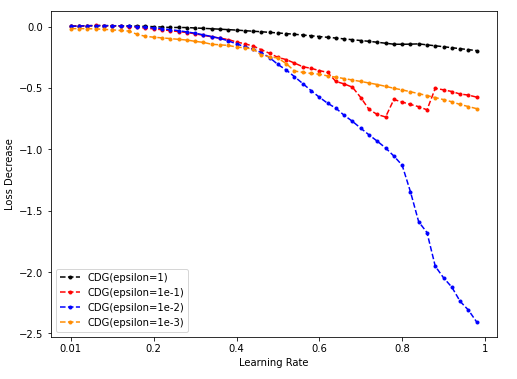
-
Dim = 32
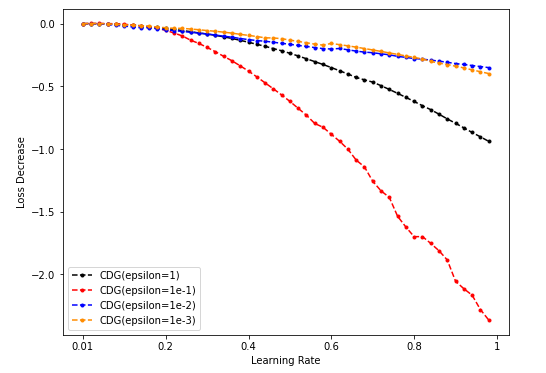
-
Dim = 64
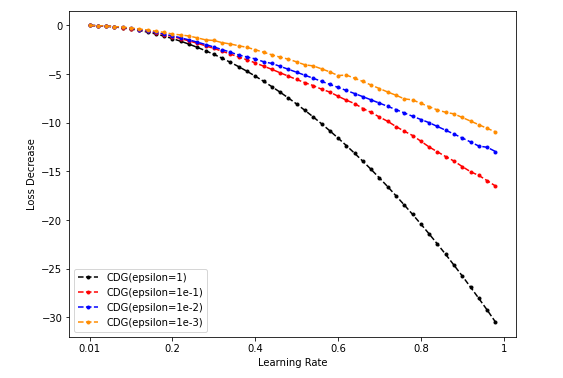
-
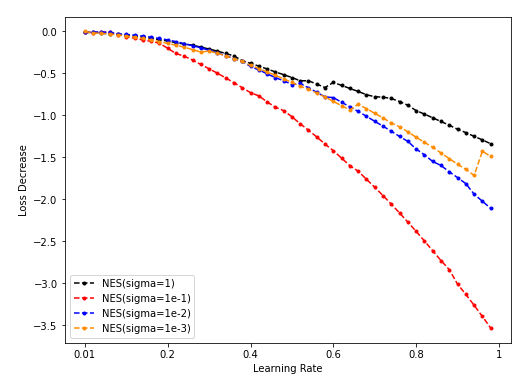
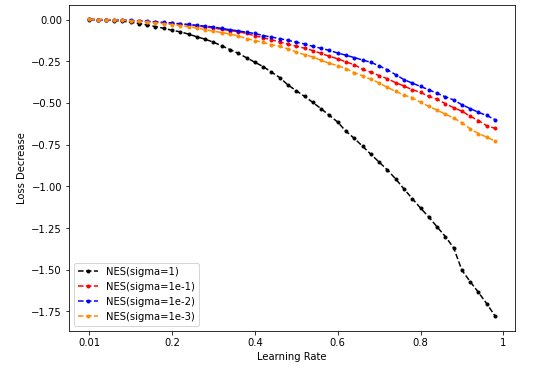
- NES lr-loss decrease plot
-
Dim = 8 Sample = 500
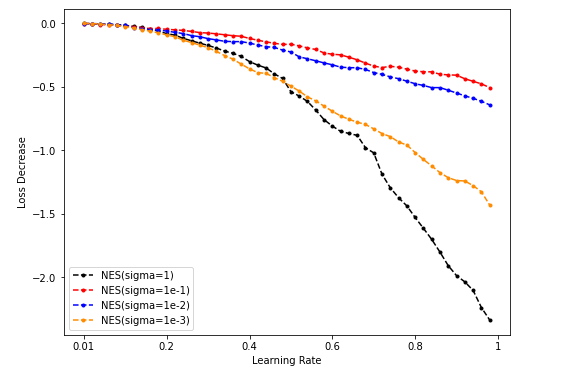
Sample = 5000
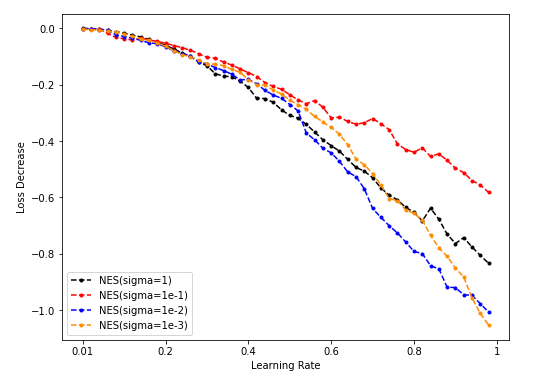
Sample = 50000
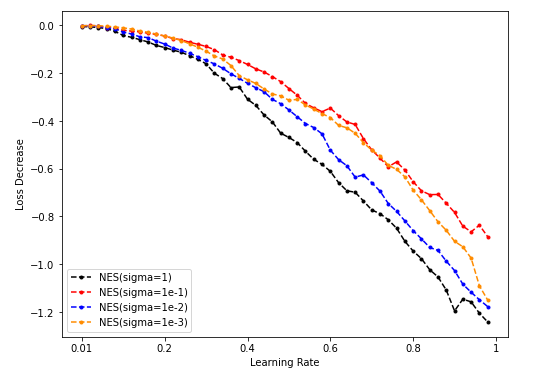
-
Dim = 16
Sample = 500
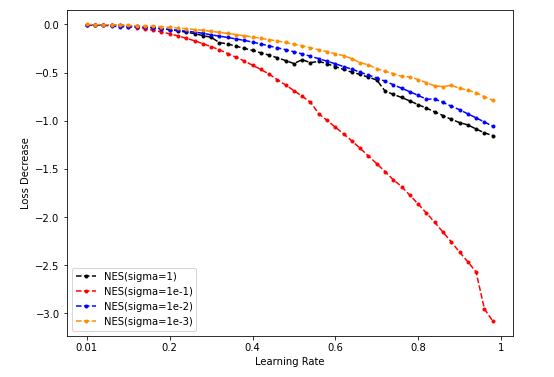
Sample = 5000
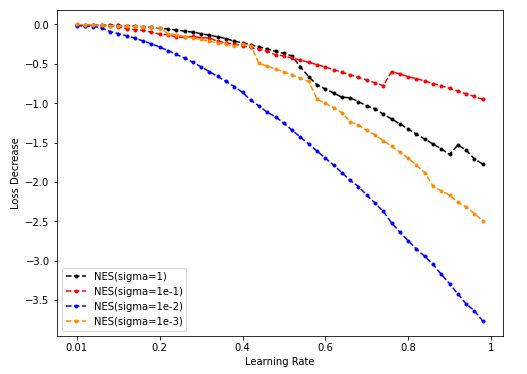
Sample = 50000
-
Dim = 32
Sample = 500
Sample = 5000
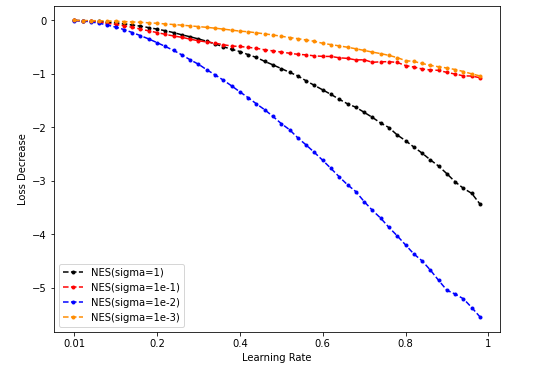
Sample = 50000
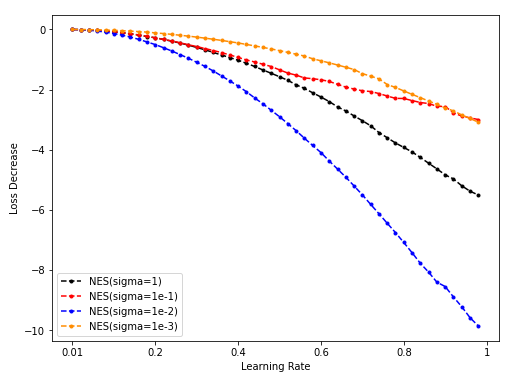
-
Dim = 64
Sample = 500
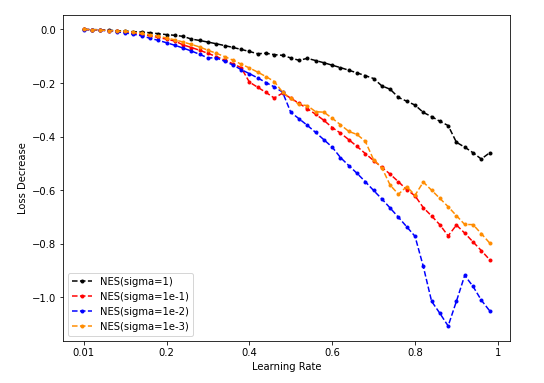
Sample = 5000
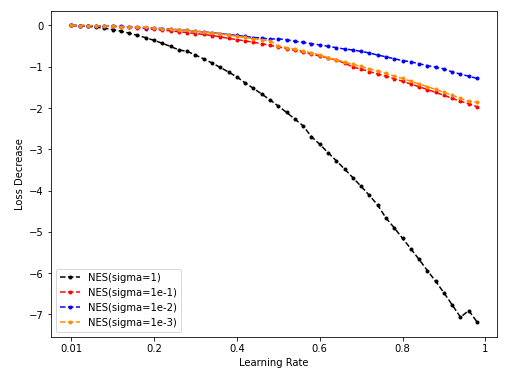
Sample = 50000
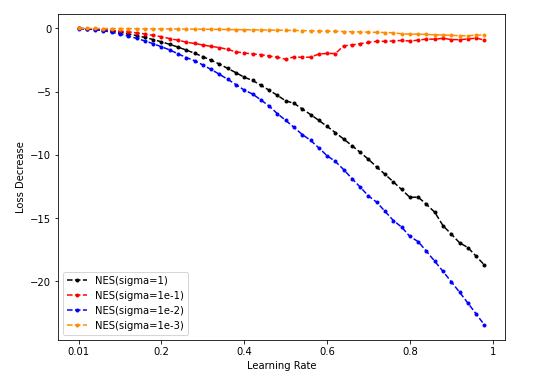
-
Thin ResNet-18 CDG grad实验 - 1
实验设置:
- 标准XNOR-ResNet-18深度,但是initial channel分别设置为8/16
- 通过STE预训练
ABOLISHED
- Binary Weights & Binary Activation case
- initial channel = 8
(从输入端算起)第1层,kernel size=8*8*3*3
(从输入端算起)第8层, kernel size=16*16*3*3
(从输入端算起)倒数第二层, kernel size=64*64*3*3
- initial channel = 16
(从输入端算起)第1层,kernel size=16*16*3*3
(从输入端算起)第8层,kernel size=32*32*3*3
(从输入端算起)倒数第二层, kernel size=256*256*3*3 Absent
- Full-precision Weights & Binary Activation case
- initial channel = 8
(从输入端算起)第1层,kernel size=8*8*3*3
(从输入端算起)第8层, kernel size=16*16*3*3
(从输入端算起)倒数第二层, kernel size=64*64*3*3
Stochastic Rounding 实验 - 1 Toy Model part
- Stochastic Rounding流程:
- (预训练模型)
- 输入一个input,对于evaluate model每一层的输出(Activations,A),(另一种方法?)分正负分别除以
torch.abs(torch.max(A))/torch.abs(torch.min(A)),将A的取值范围映射到[-1, 1],再对A加1除2,得到[0, 1]上的A作为prob,设定temperature进行relaxed Bernoulli采样,采样值取值范围为[0, 1],减去0.5后通过sign得到stochastic rounding activation - STE-like forward & backward
- Exp on raw model
-
batch size = 640k


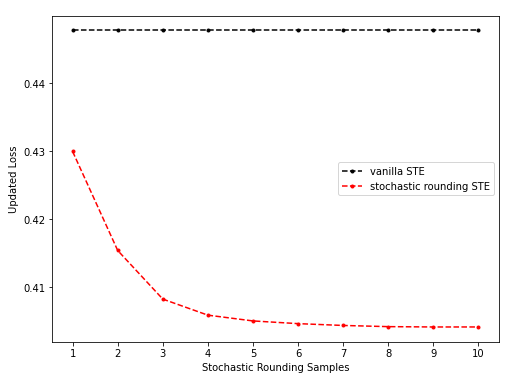
-
batch size = 256
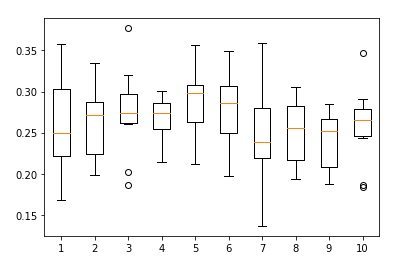
- Exp on pretrained model
- 使用STE进行预训练,batch size = 16k,训练500step(至loss不再有明显下降)
-
batch size = 256

Discussion
Mr.Chen:
- FP model上测试CDG/NES算对了(https://en.wikipedia.org/wiki/Rosenbrock_function)
- 还可能是平滑后的梯度指向的不是loss decrease的方向/平滑本身有问题
- 不找平滑之前的函数的最佳方向了/离散函数的方向 - NES max point(sample之后normalize,看哪个点下降最快)
- Stochastic rounding 前传 量化的图 随机性
- 在STE grad上做扰动,找loss下降最快的点
- STE backprop改成随机的。
妃哥:
- sr-STE更新后用vanilla STE/不引入随机性地看更新后loss的情况