2021/4/30结果反馈与讨论记录

2021/4/30

XNOR-Res18 Finetune

数据采集方法：后 10 epoch 算术平均

Width Weight Decay Training Loss Training Accuracy Validation Accuracy
96 0 1.6725e-3 0.9995 0.9257
192 0 0.04267 0.9847 0.9019
192 1e-4 0.1164 0.9599 0.9042
192 5e-4 0.6245 0.7863 0.6048
192 5e-5 0.05670 0.9810 0.9152
192 1e-5 0.02194 0.9921 0.9121
192 5e-6 0.02111 0.9929 0.9178
192 3e-6 0.02237 0.9925 0.9080
192 1e-6 0.02861 0.9904 0.9069
256^1^ 0 0.1364 0.9520 0.8583
256^2^ 1e-5 0.4476 0.8434 0.7964
    1. The bs of the case init channel = 256 is 64.
    1. bs = 64, lr = 2e-3.

NES Applied to Naive MLP

Pseudo code:

  • 初始化目标模型target model(直接初始化weights)、评估模型evaluation model(认为是Guassian, 初始化每个参数对应分布的μ和σ)
  • 在同一个batch内(same input)：
    • 对于评估模型中的每一个参数(weight):
      • 采样M次(M对应population，就是MC sample的数量):
        • 每次采样后，计算fitness，计算log-derivatives ${\nabla}_\theta log π(\mathbf z_k|θ) $
      • 根据M次采样的结果，计算${\nabla}\mu J$ 和 ${\nabla}\sigma J$ ，计算Fisher info matrix(简单起见单独计算μ和σ的两个F值)
      • 更新${\mu}$和${\sigma}$

Q1: evaluate模型最后的weights是什么？能想到的：以μ为最后的weights(并量化)或者从学到的分布中采样(并量化)
Q2: fitness用loss合适吗？按说应该表现越好reward越高，所以fitness也越高，但是loss和这个过程正好相反？
Q3: weights 分布必须依次采样并更新，不能并行进行？

Experiment Results

Parameters & Settings

  • num_init=3 考虑到模型参数初始化对结果的影响很大（随机性很强），对模型进行若干次初始化，分别测试并对结果取平均。
  • num_dim=[2, 4, 8, 16, 32] 实验模型是一个三层MLP，每层MLP上neuron数量为num_dim。
  • num_batch=10 每次初始化模型后使用若干batch计算梯度，每一batch维度符合(160000, num_dim)，数据i.i.d.采样自N(0, 1)。

Quick Check

作图说明：

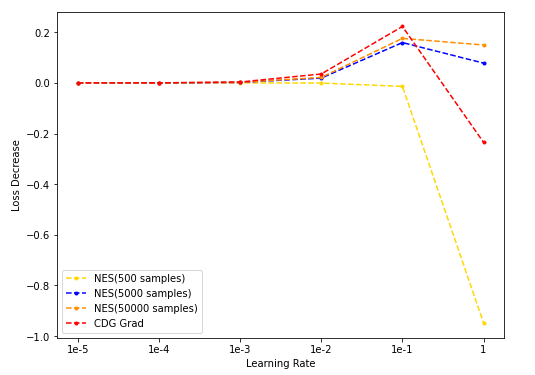
  • lr固定为0.1；
  • Loss decrease 表示loss下降的绝对值；

三张图分别为：

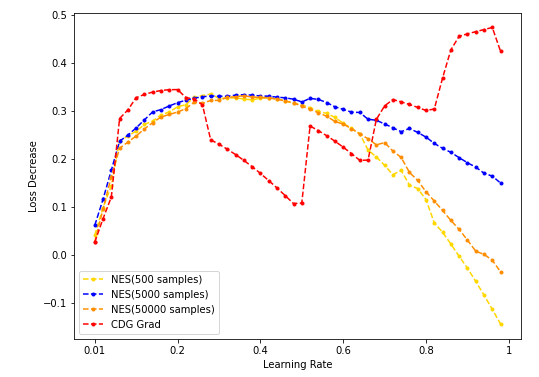
  • NES采样数分别为500/5000/50000时计算出的grad用于梯度下降，与CDG grad用于梯度下降的结果对比：

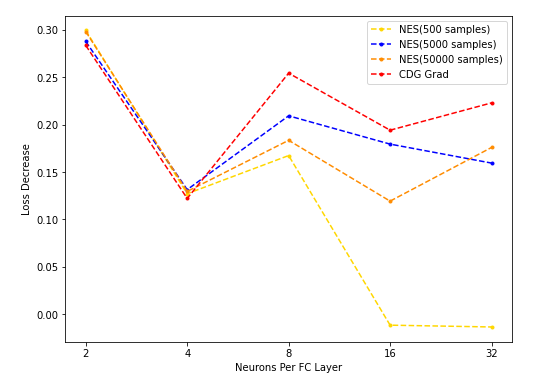
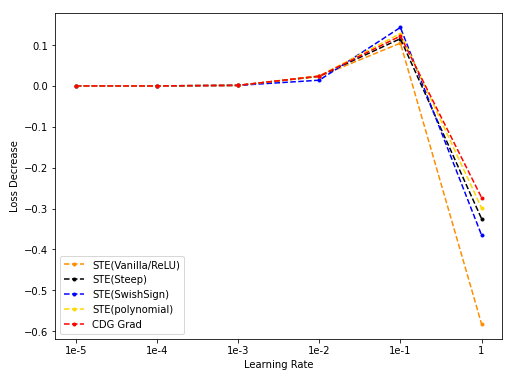
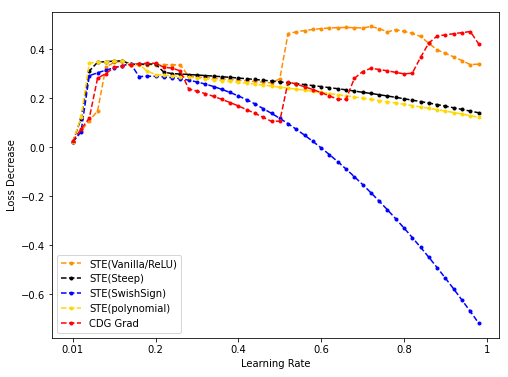
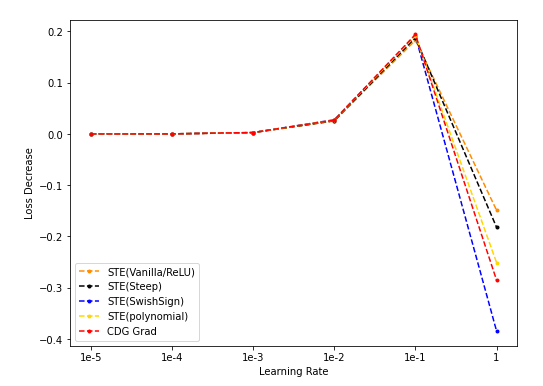
  • 不同的STE(vanilla/ReLU, Steep, SwishSign, Polynomial) grad梯度下降，与CDG grad用于梯度下降的结果对比：

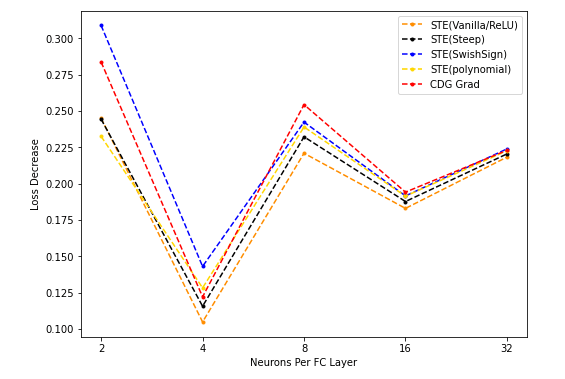
其中不同的STE的形式为（自BinaryDuo）：

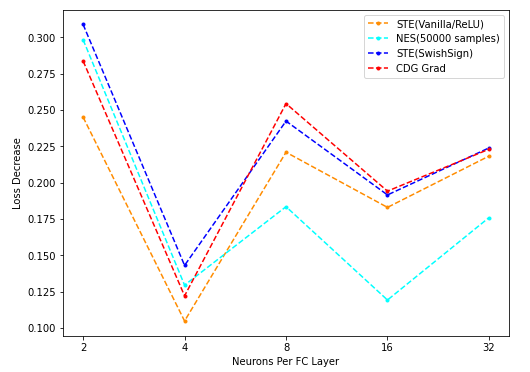
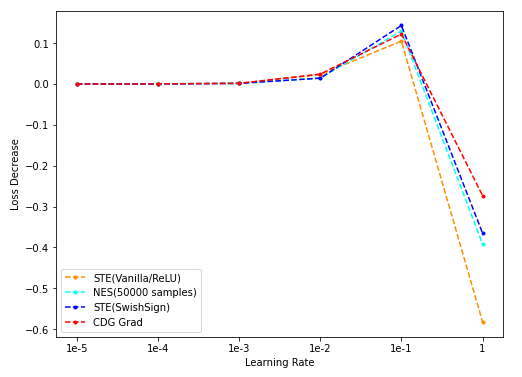
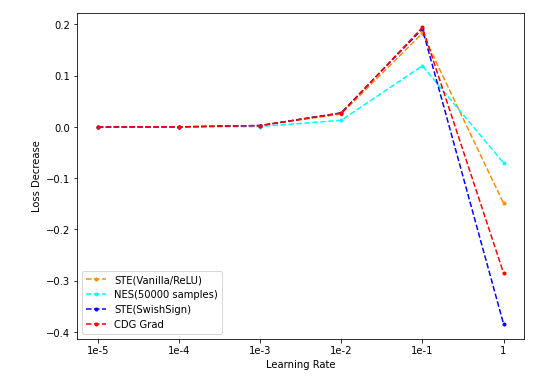
  • 将STE(vanilla/ReLU)、STE(SwishSign)、NES(population = 50000)、CDG grad的下降结果在同一张图中描绘：

Fix num_dim, Loss Decrease - lr Plot

作图说明：

  • 每组折线对应同一num_dim；
  • Loss decrease 表示loss下降的绝对值；
  • 受到采样时间的限制，在[1e-2, 1]区间replot的数据是num_init=1的条件下取得的，应当留意可能存在的随机性。

观察[1e-5, 1e-4, 1e-3, 1e-2, 1e-1, 1]尺度上的Loss decrease判断出loss decrease - lr最佳区间应在[1e-2, 1]内，因此在[1e-2, 1]区间内重新扫描。

num_dim = 4

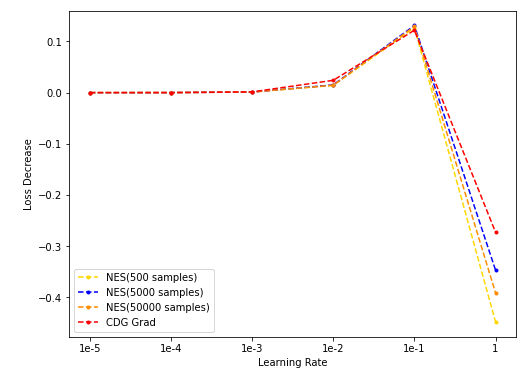
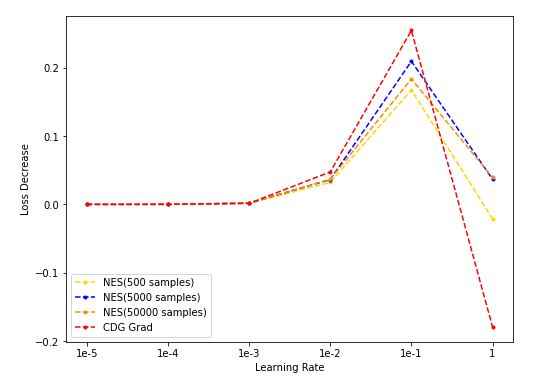
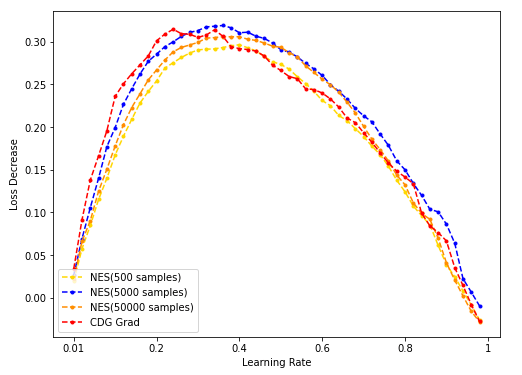
  • NES(500/5k/50k采样)与CDG baseline:

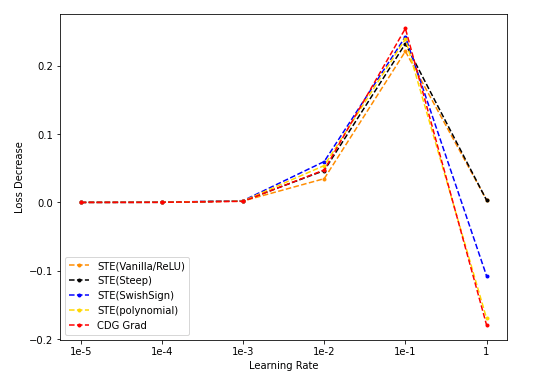
  • STE(vanilla/Steep/SwishSign/Polynomial)与CDG baseline:

  • NES(50k采样)/STE(vanilla/SwishSign)与CDG baseline:

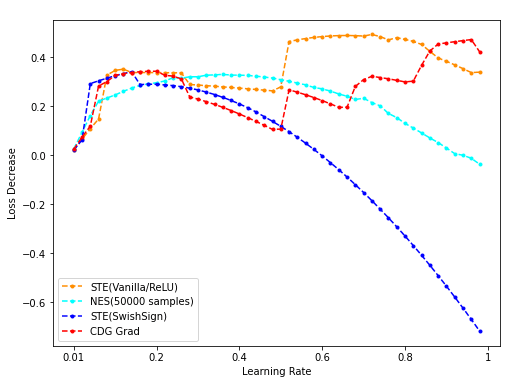
num_dim = 8

  • NES(500/5k/50k采样)与CDG baseline:

  • STE(vanilla/Steep/SwishSign/Polynomial)与CDG baseline:

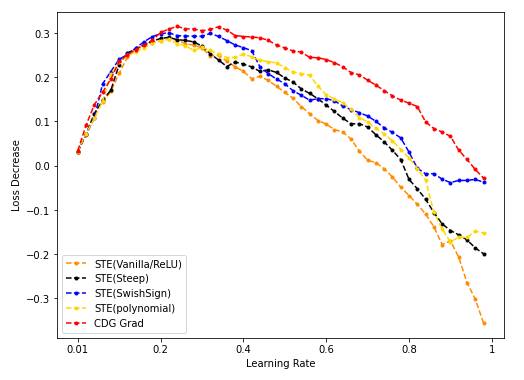
  • NES(50k采样)/STE(vanilla/SwishSign)与CDG baseline:

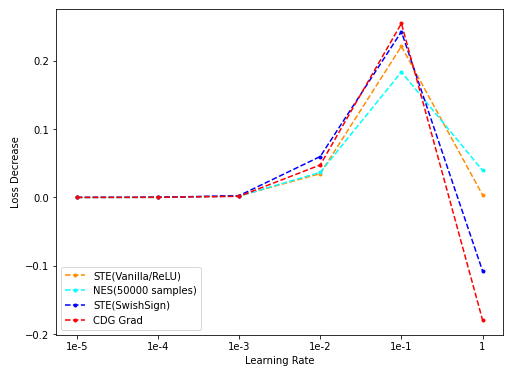
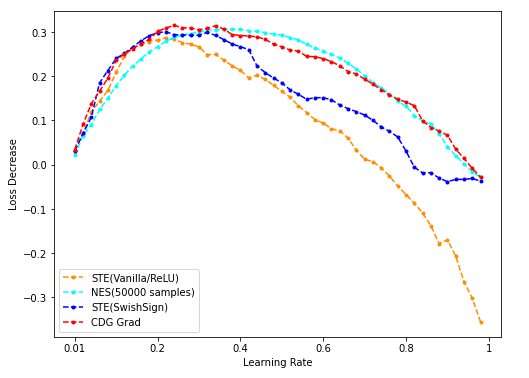
num_dim = 16

  • NES(500/5k/50k采样)与CDG baseline:

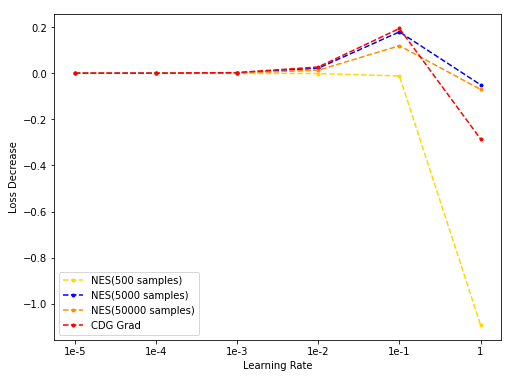
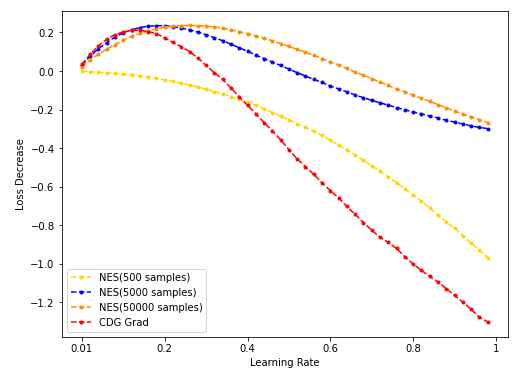
  • STE(vanilla/Steep/SwishSign/Polynomial)与CDG baseline:

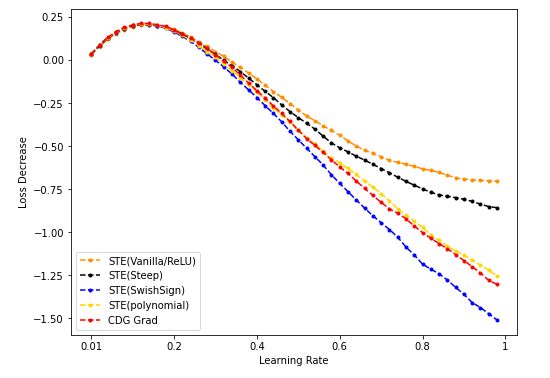
  • NES(50k采样)/STE(vanilla/SwishSign)与CDG baseline:

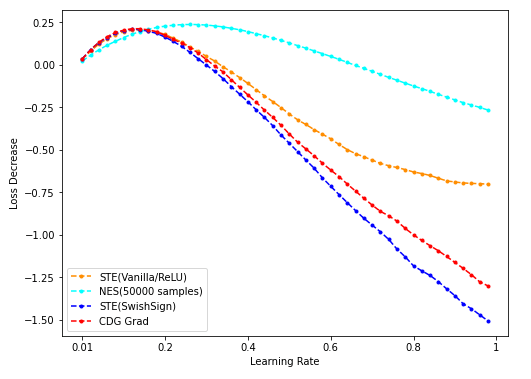
num_dim = 32

  • NES(500/5k/50k采样)与CDG baseline:

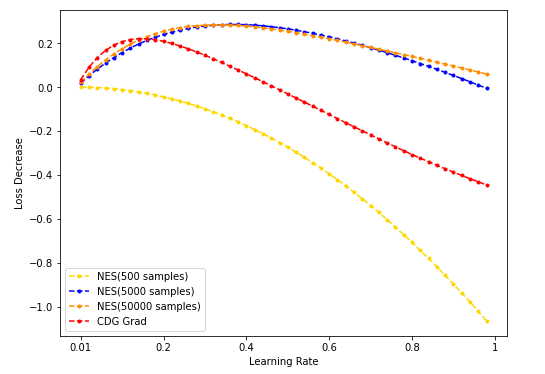
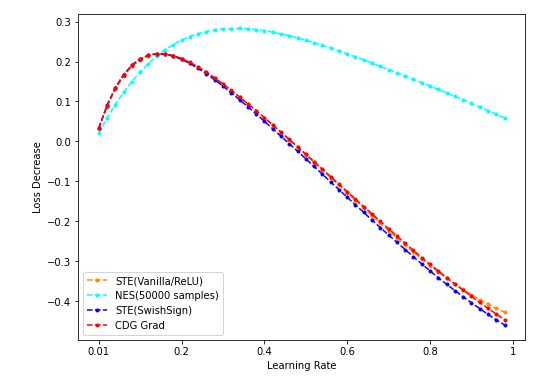
  • STE(vanilla/Steep/SwishSign/Polynomial)与CDG baseline:

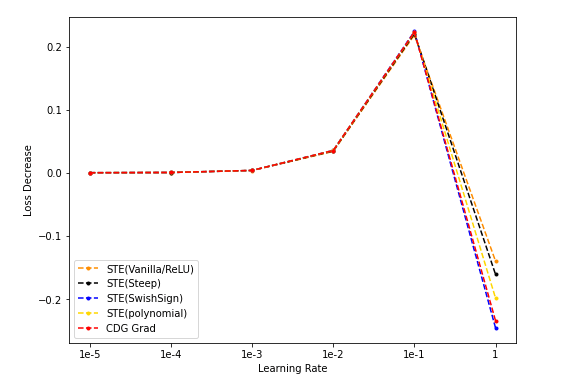
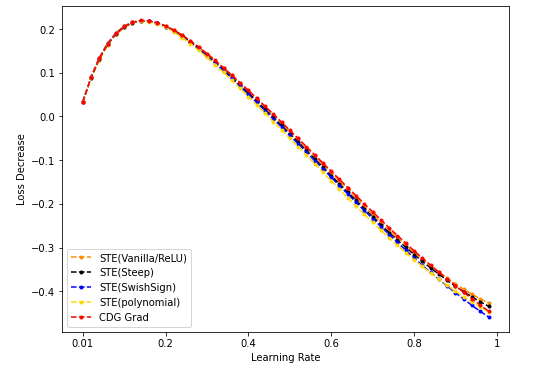
  • NES(50k采样)/STE(vanilla/SwishSign)与CDG baseline:

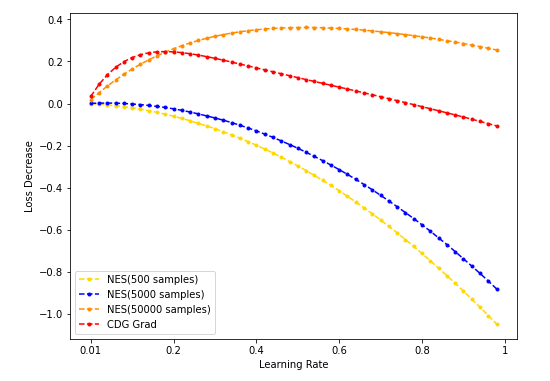
num_dim = 64

  • NES(500/5k/50k采样)与CDG baseline:

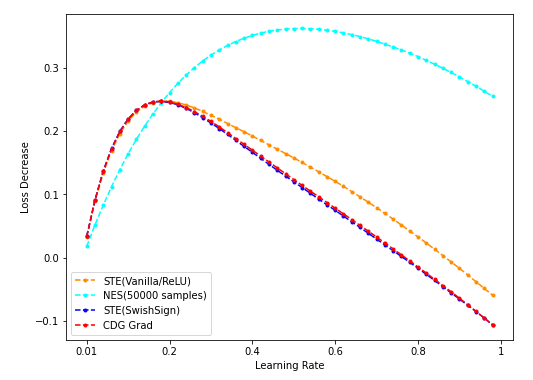
  • STE(vanilla/Steep/SwishSign/Polynomial)与CDG baseline:

  • NES(50k采样)/STE(vanilla/SwishSign)与CDG baseline:

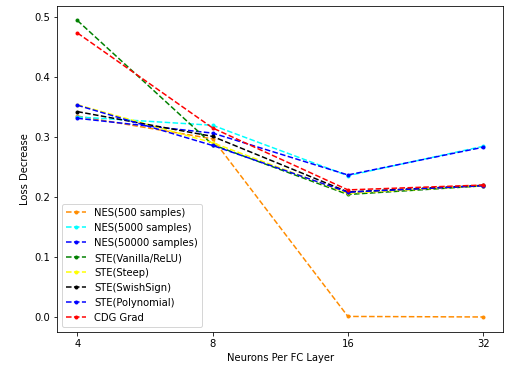
Best Loss Decrease w.r.t. num_dim

一个显而易见的现象：num_dim越少，loss受到binarize的影响越大。（因此dim较少时的结论可靠性也更低）
作图说明：

  • 在每一dim，每种梯度估计方法的数据中选取适当的lr，使得该方法下降的loss最多(即按照最佳lr/最佳loss下降绘图)。

Discussion

  • 训练后期？方向？

  • 采样方法：
    • STE方向为mean
      Q：lr固定？步长不一样。

    • 不同STE方向张成的线性空间中找(density可能不是高斯的——均匀?)

    • more complicated…

  • particle filter/marcov chain

  • STE随机化？（BP）
  • STE训练到局部最小值时切换到NES

To-Do List

  • ResNet CDG 单层loss下降
  • sigma?
  • dataset UCM / CIFAR-10
  • 训练阶段 ResNet(训练收敛，维度太高可以找某一维)
  • 横坐标是超参，loss下降是纵坐标 UCM