Learned Step Size Quantization

2021/9/30

来源：ICLR20
resource：github上备份的包括ipad标注的pdf版本。
作者是IBM Research的Steven K. Esser等人。

Summary：本文提出将scale（文中称为step size）作为可学习参数引入量化训练，并对梯度进行调整使得网络参数与量化参数的训练同步，同时，本文的优化目标不是最小化量化误差，而是最小化task target，我认为这种思路很对劲。

文章贡献：

新的可训练量化参数Scale。
对梯度进行scale，弥补量化参数和网络参数梯度的差异。

Rating: 4.5/5.0 朴实好文！简单有效！
Comprehension: 4.3/5.0 基本上能懂，而且后面甚至放了伪代码帮助理解，他真的想让我懂！

1 Introduction

有一些facts可以参考下：

早期的低精度神经网络使用简单固定配置的量化器，后续的工作开始使量化器适应数据，基于数据分布的统计特性或者减少训练时的量化误差，在LSQ工作的近期涌现了QAT。
减少量化误差的方案未必是最佳的（倒不如说大概率不是最佳的吧），因为可能有一套完全不同的量化参数使得task loss更低。

2 Mehtod

一些记号和说明。不是很自信，还是放出来：

以及计算流图，MQBench的已经很清楚了，当然这个也不差：

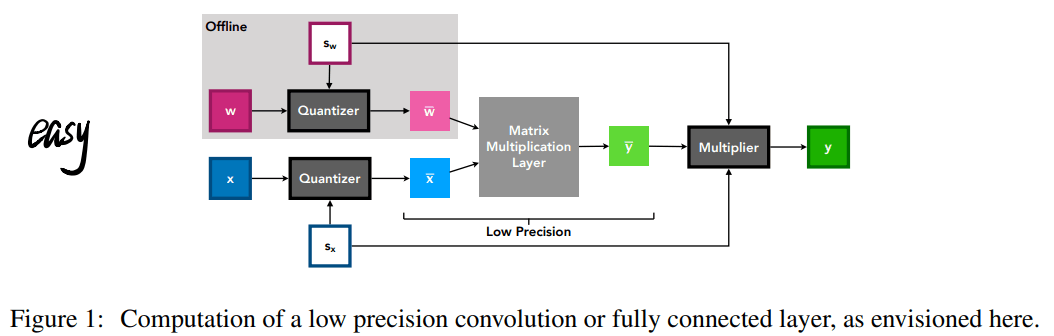
2.1 Step Size Gradient

设计了一种对于scale的梯度：

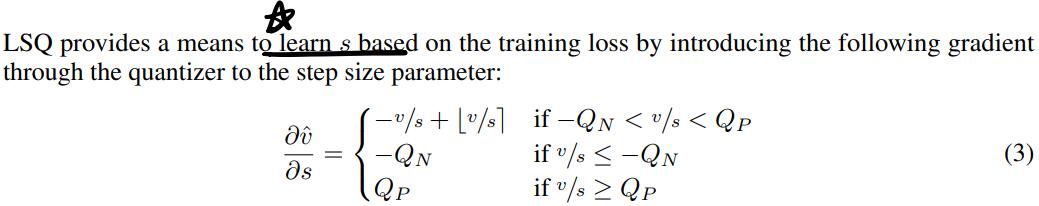
对应的梯度长成下面这个样子：

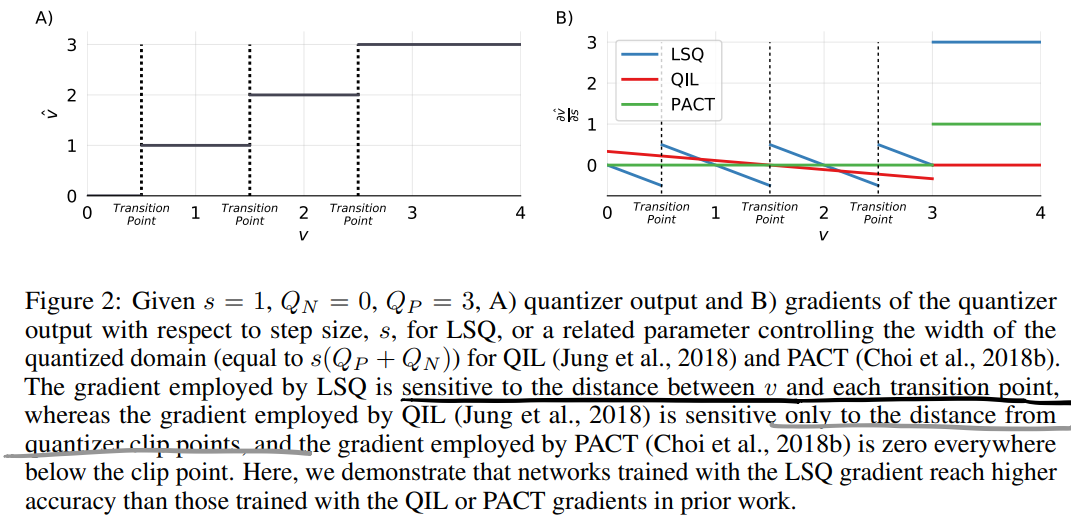
上图的一句话不是非常理解，图B是量化器输出关于step size的梯度，对于LSQ而言是s，而对于QIL和PACT而言是一个相关的控制量化域的参数，等于s(Q_p+Q_n)，疑惑，这里LSQ的量化域就不是这个了吗？量化后数据的分布长度也是啊？
此外，LSQ的梯度对待量化数据与每个状态转移点之间的距离非常敏感，其他方法要么是0，要么就很平缓。
而至于为什么要考虑被量化数据和量化点之间的距离问题，作者说数据和量化点距离越近就越容易因为s的更新发生翻转，因此认为当v与转换点距离减小时\(\frac{\partial \hat{v}}{\partial s}\)的值增大（说实话我没想明白。）。
有个s的初始值，感觉没太有作用。

2.2 Step Size Gradient Scale

作者指出更新平均幅度和对应参数的幅度成比例时能够有效收敛，因此，作者希望scale的梯度和幅度的比值与参数的梯度/幅度比值接近，即下式近似为1：

考虑到精度上升时scale减小，量化项增多时scale update增大（反传时加在一起的item也变多了），所以要对梯度进行校正：

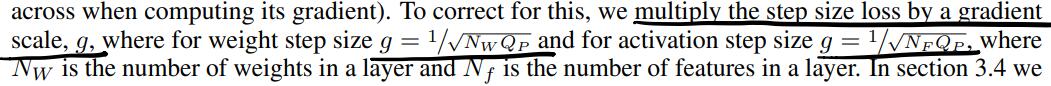
校正项与number of weights per layer有关，具体需要check下MQBench中的实现。
在Appendix A有比较粗糙的证明，~~好像BN对这个scale项也有说法~~ -> activation之前有BN，假设BN scale参数的更新是量化前激活值变化的主要驱动原因，可以按照与之前类似的方法证明act中也有类似的不平衡 -> 所以没有BN怎么办？需不需要自己测一下scale的梯度？

2.3 Training

一些细节：首层尾层还是8-bit，从预训练模型初始化。

3 Result

3.1 Weight Decay

减少模型的精度会减轻模型过拟合的趋势，从而降低使用WD的必要性。

3.4 Step Size Gradient Scale Impact

不scaling时相对parameter size，对scale的更新的幅度比weight的高2-3个数量级。

3.6 Quantization Error

从三个不同的误差角度出发，LSQ都不是缩小量化误差，因此直接让量化器拟合数据分布(应该指的是被量化的数据)不是最优选择，不见得取得最佳task loss（好喷！）

3.7 Improvement with KD

KD可以帮助低精度网络追上高精度网络性能。为了与前面不矛盾，我理解这里是非参数的对齐，而是对特征图的对齐。

Appendix B

太棒了！有很多实现细节！