PACT: Parameterized Clipping Activation for Quantized Neural Networks
2021/9/2
来源:arxiv18
resource:github上备份的包括ipad标注的pdf版本。
作者是IBM的Jungwook Choi, Zhuo Wang, Swagath Venkataramani, Pierce I-Jen Chuang, Vijayalakshmi Srinivasan, Kailash Gopalakrishnan等人,这篇文章属于是量化领域的经典文章了,最后居然没有中,可惜。
Summary:提了一个量化act的简单方案,就是给ReLU加一个可学习的clip threshold。结果意外地有效,在W4A4的情况下可以保持与FP非常接近的效果。方案过于简单以至于总结都写不了太多。
Rating: 4.0/5.0
Comprehension: 4.5/5.0
1 Introduction
- 引入的clip threshold相比不截断的ReLU量化误差更小,但是范围又比一般的clip函数大,保证了梯度的传播。
3 Challenges In Activation Quantization
- 有些比较玄乎的说法:
- 量化参数等效于离散损失函数关于参数变量的假设空间,因此可以通过模型训练补偿参数量化误差。
- 当使用ReLU作为激活函数时量化会更困难,因为ReLU有个很大的动态范围。
- 很难确定一个全局clip threshold(不难理解)。就算取一个比clip更大的全局threshold,相比一般不量化的relu也会有很大的量化误差。
4 PACT: Parameterized Clipping Activation Function
Pact的公示表示:
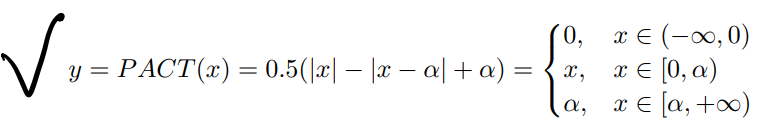
重建结果表示(回忆一下自己举的例子?):
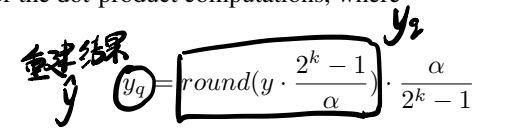
导数的表示有些抽象,我至今没看懂这个x是什么。是输入的参数还是alpha本身?:
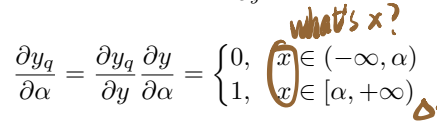
4.2 Exploration of Hyper-parameters
- 一些细节:
- alpha最好的尺寸是每层一个,appendix里面有消融实验(per-channel不好挺意外的,但是对量化来说确实per-tensor更经济些)
- 根据Appendix,alpha的初始值如果太小,则大多数act落入非0梯度区间,会导致早期epoch中alpha不稳定;而alpha的初始值如果太大,梯度就会太小而使alpha卡在一个较大的值上。
- alpha的正则化参数和参数的l2超参一样最好,如果比特精度高的话这个正则化超参要scale小一点。
- 第一层和最后一层没有量化。Appendix里说8-bit量化初始层与最后一层精度下降很小。
- 只把ReLU替换成了PACT,但是其他超参没有变化,train from scratch。
5 Experiments
- 一些显而易见的结论:
- 只量化Act时:
- 4A就接近FP精度了;
- A位宽越高精度越高。
- 用DoReFa量化W,A采用PACT方案时:
- 4A4W可以达到 \leq 1 FP精度的性能;
- Appendix里说PACT允许参数有更剧烈的量化。
- 只量化Act时:
6 System-Level Performance Gain
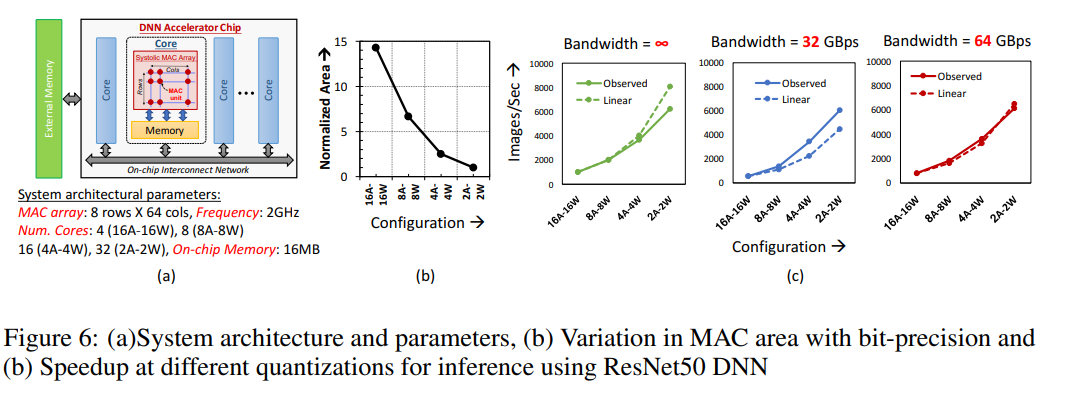
- 一些比较玄乎的结论:
- 当W/A从16-bit转变为2-bit的时候芯片密度有~14x的增益(核数增多)
- 实际系统的增益有一种超线性的表现(比如4x FLOPs但是4.5x性能提升),这是因为数据可以存在核内存中,避免了数据外部搬运。