ZeroQ: A Novel Zero Shot Quantization Framework
2022/1/21
来源:CVPR20
resource:github上备份的包括ipad标注的pdf版本。
作者是北大和UC Berkeley的Yaohui Cai, Zhewei Yao, Zhen Dong, Amir Gholami, Michael W. Mahoney, Kurt Keutzer等人,KK好像是领域大佬哎。
Summary:本文提出了一种严格不要数据的PTQ方法ZeroQ(一般的PTQ算法可能需要无标签数据计算act的scale)。具体而言,ZeroQ本质上是一种Mixed-precision方案,利用FP model和对应层量化的模型输出之间的KL散度作为敏感度。由于本文面向严格无法获得数据的场景,作者提出从BN层统计信息中"蒸馏"数据的方法,做法是将0均值、单位方差的高斯数据喂入FP模型,计算该batch生成的数据在模型各BN处的均值与方差,用L2 norm和BN中原始统计信息对齐,并在反传中更新该batch生成数据,更新结束后,即可利用"蒸馏"出的数据计算量化敏感度。在统计各层敏感度后,采用朴素的动态规划方法确定MP方案(文中称为Pareto frontier方法)。(测敏感度的方法有一点改进,简言之是对各层分组,在各层独立测量与全方案空间遍历之间找一个比较经济的方式)此外,作者在很多模型+检测任务上进行了测试,除性能不错外,该PTQ方法另一大突出优势是很快(作者称8卡V100环境下可30s量化ResNet50)。
文章贡献:
- 一种启发式Mixed-Precision PTQ方式,对敏感度分析有小改进;
- 利用BN的统计信息生成"蒸馏"数据,用于act截断值与敏感度测定(而不需要接触任何数据)。
Rating: 3.5/5.0 一般。
Comprehension: 4.5/5.0 简单。
1 Introduction
- 又给了一个喷QAT的借口:在线训练的场景。
2 Related Work
- 喷ACIQ等对act的量化是per-channel的
有这回事?揍他狗*的
3 Mehtodology
- 用了非对称均匀量化方案,参数与激活值都是朴素量化(min-max,后面也有percentile的尝试)。
- 提了一个观点:mixed-precision是极低比特(例如4-bit)取得高性能的关键。
3.A 敏感度测定
把数据同时喂入全精度模型和某一层被量化成k-bit的模型,以两个模型输出的KL散度作为敏感度(该值越小越好):

原文还有一张图,但是我感觉挺简单的(总之还是放出来):
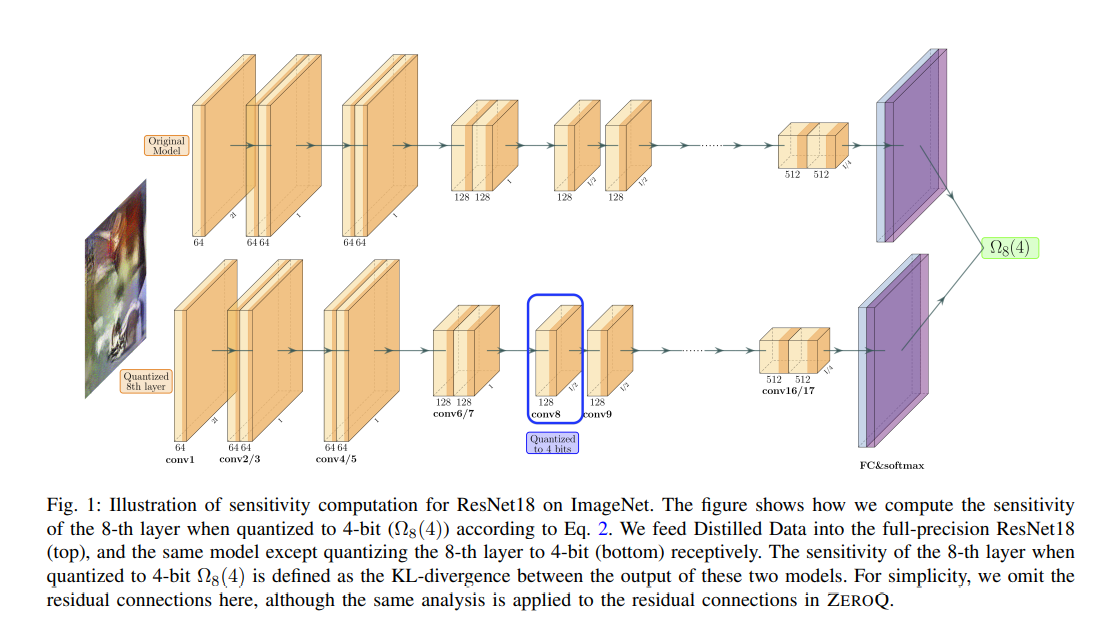
3.B 数据蒸馏
为了解决完全没有数据的问题,作者提出利用BN层中的统计数据生成"蒸馏"数据用于激活值截断阈值确定与敏感度分析,具体做法是将服从N(0, 1)的数据喂入模型,对齐在各个位置的统计信息,更新得到所需数据:

对应算法为:

3.C Mixed-Precision方案
本质上是一个动态规划方案:

根据上式可以画出一条帕累托曲线,这里认为最低的敏感度=最佳量化性能,即在帕累托曲线上根据所需模型size取量化方案(注意,后面和其他方法比时,也是以模型size/MB为标准,而不是量化位宽->也好理解,毕竟这是MP方案),图中每个蓝点都是一个MP方案:
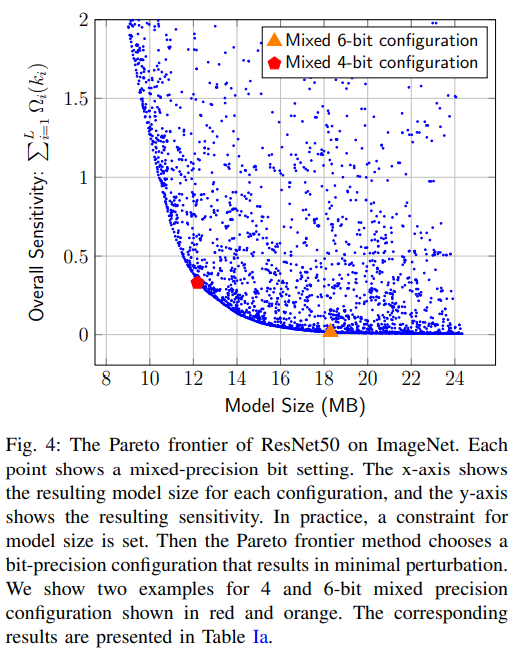
在敏感度分析时有一点小trick,作者在各层独立测定与遍历全模型量化方案测定之间找了个trade-off,即分组迭代测量敏感度:

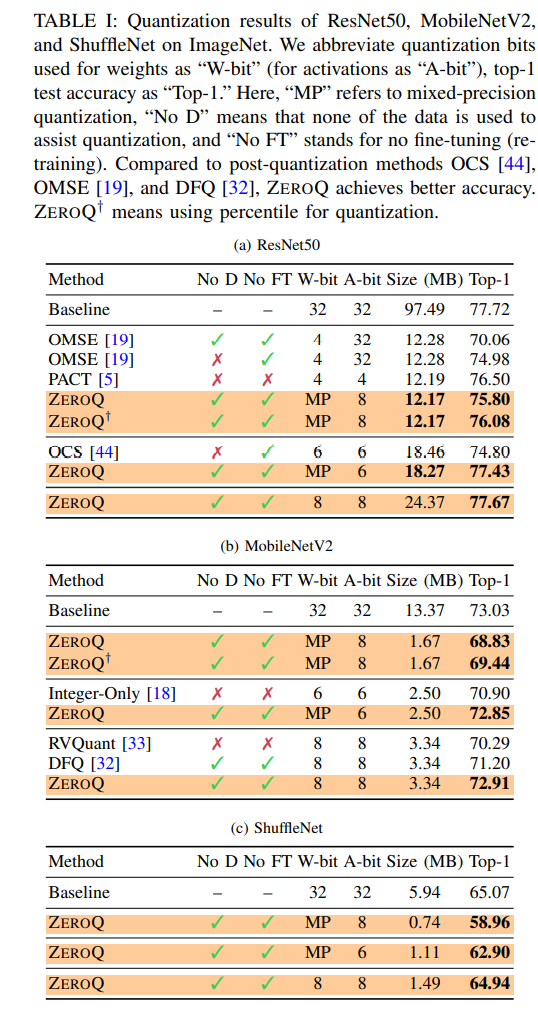
4 Results
主要贴一下大实验,考虑到这是CVPR20的文章,他们主要和DFQ比,效果在当时看还不错: