MQBench: Towards Reproducible and Deployable Model Quantization Benchmark
2021/9/2
来源:NIPS2021
resource:github上备份的包括ipad标注的pdf版本。
作者是商汤的工具链团队,包括Yuhang Li, Mingzhu Shen, Jian Ma, Yan Ren, Mingxin Zhao, Qi Zhang, Ruihao Gong, Fengwei Yu, Junjie Yan等人。
Summary:尽管现在有很多的量化算法,但是学术上提出的新方法因为训练pipeline没有统一,且忽视了硬件部署的要求(意思大概是硬件库不支持?),他们的结果通常无法复现,或者无法部署。所以他们做了这个Model Quantization Benchmark工作来评估模型量化算法的复现与部署能力。结果发现不同的学术量化算法性能非常接近,且没有明显的优劣关系(有些性能提升主要是通过改进训练达到的,这里点了DSQ的名,好狠,连自己主管的工作都diss)。
Rating: 3.5/5.0
Comprehension: 3.5/5.0
1 Introduction
- 据说在W3A3的情况下就能达到FP accuracy了,哈人( Learned step size quantization)
- 文章提了两个在量化算法研究中长期被忽略的点:
- 超参数设置对量化网络的性能影响很大,比如lr、wd和预训练,所以他们对齐了训练管道
- 大多数学术研究没有在硬件设备上部署算法,比如没有fuse BN、有些算法只量化了输入和参数(而没量化element-wise add和concate),同时还有鲁棒性的问题(比如算法是per-tensor设计的,但是用到per-channel情形),因此学术研究和真实部署之间有较大的gap。
2 MQBench: Towards Reproducible Quantization
- 在复现性方面的评估包括给定硬件支持的推理库、量化算法、网络结构和比特位宽。
- Hardware-aware Quantizer:
- 本文只关注均匀量化,非均匀量化需要特殊的硬件设计。
- 均匀量化的quantization op和dequantization op可以用下式表示,其中s和z分别是scale(实数)和零点偏移(整数):
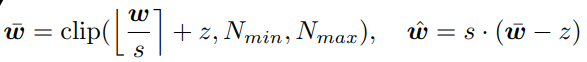
- 这些量化方案可以进一步分为:
- 对称与非对称量化
- per-tensor与per-channel量化(前者是对整个layer,后者是更细粒度的量化)
- FP32 scale与power of two scale,前者几乎连续(nearly continuous),后者更难些,但是可能会进一步加速。
- Hardware Library报菜名:
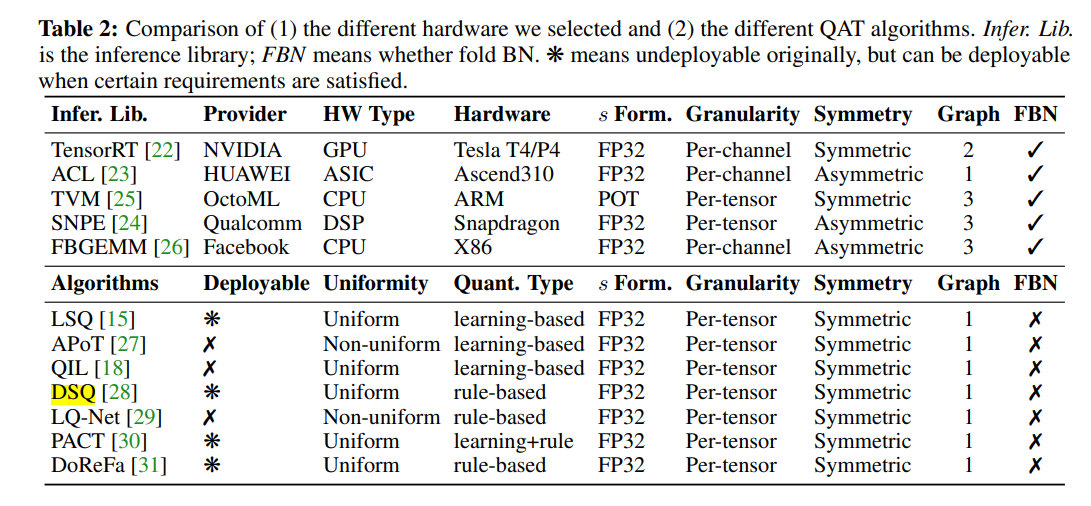
- 细节设置:
- Bitwidth里说他们对算法的仿真是fake quantizaiton,因为在通用硬件上不能部署所以没实验3-bit的情形,在硬件设置下2-bit不收敛。
- 实验用相同的pre-trained model初始化。
3 MQBench: Towards Deployable Quantization
这部分总体还挺有用的。
3.1 Fake and Real Quantization
仿真中的Fake Quantize与部署中的Real Quantization:
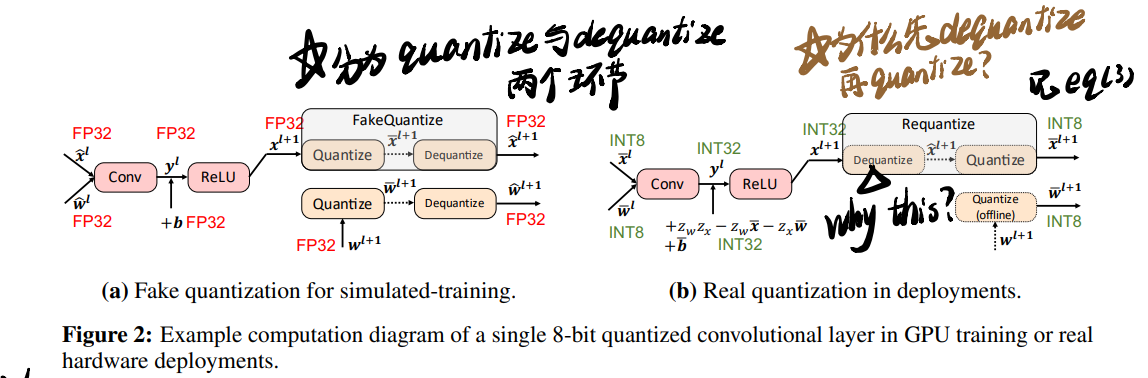
在GPU上做QAT的时候实际上是用FP32仿真量化过程(也就是Fake Quantize),在部署的时候则是使用只有整数运算的Real Quantize。这个过程可以用公式表示为:
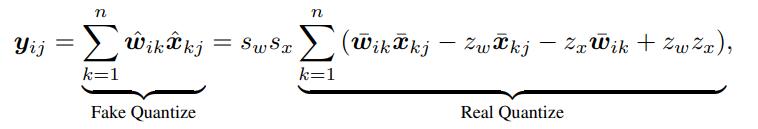
下面对requantize的定义则解释了上图右侧的疑问:
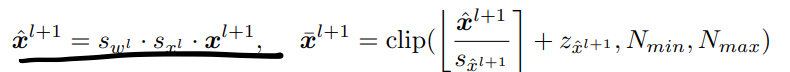
在实际部署中,两个int8的数的计算结果是个int32的数,进一步经过激活成为\(x^{l+1}\),还是个int32的数,通过scale恢复FP32的数,再量化回8bit的数,进行下面的运算。上式(2)里real quantization括号里的最后两项可以离线计算,因为参数和\(z_w\)与\(z_x\)在量化前就已经能确定了(但是\(z_w\)和\(z_x\)是啥啊)
因为仿真和实际部署的计算图里有些细微的差距(在哪?)所以最终结果也有一些区别。
3.2 Folding Batch Normalization
- BN的作用包括
reduce internal covariate shift and also smooth the loss surface for fast convergence - BN可以和Conv中的参数merge起来:
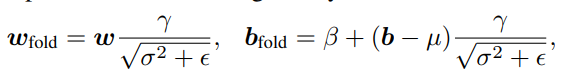
- 有五种常见的BN folding策略(式中\(\gamma\)和\(\beta\)分别表示仿射变换的参数和偏移,\(\mu\),\(\sigma^2\)分别表示running mean和variance,\(\epsilon\)是数值稳定引入的工具变量,\(\tilde{\mu}\), \(\tilde{\sigma}^2\)表示当前batch上的均值与方差):
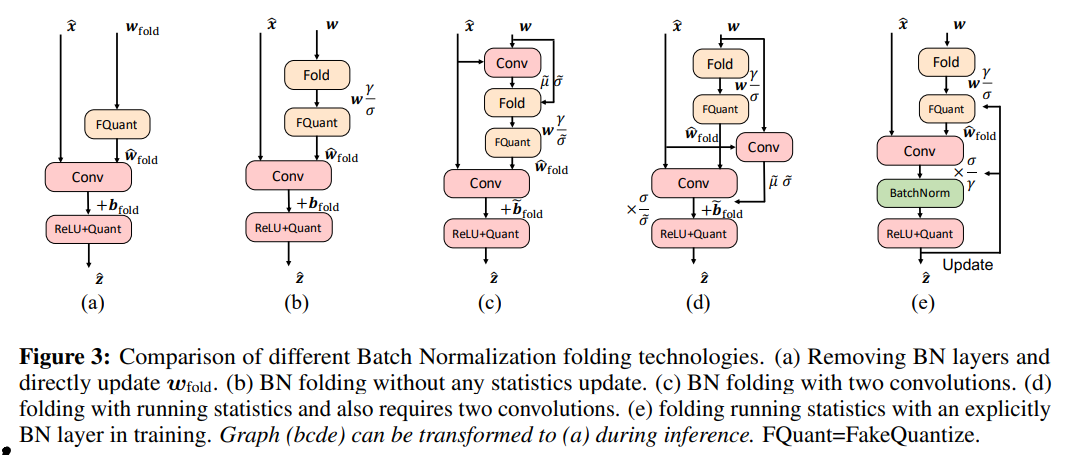
- Strategy 0:直接把参数融进去,但是取消BN有梯度爆炸现象,不能用大LR训;
- Strategy 1:merge的时候不改统计参数,但是affine transform的参数可以通过SGD更新,这个策略可以平滑loss landscape并产生差不多的accuracy,在分布式训练的时候因为不用同步统计数据而减少训练时间;
- Strategy 2:引入了额外的Conv层,第一次计算当前batch的均值与方差,并用它merge到参数中作第二次Conv,inference的时候就用running mean与variance做(好怪哦,为什么?而且里面的参数怎么取得的?所以还是有个专门计算当前batch统计数据的BN层在里面?);
- Strategy 3:哈人,更难了。同样是计算两次,且第一次计算当前batch的统计数据。但是merge的时候还会用running statistics避免波动,batch variance用来rescale第二次的输出结果;
- Strategy 4:不需要计算两次Conv但是显式地增加了一层BN,好处之一是batch statistics是用量化后的参数计算出来的。
During inference, the re-scaling of output $$\frac{\sigma}{\gamma}$$can be neutralized by BN, therefore the graph can be transformed to Fig. 3(a)(不懂)
3.3 Block Graph
这块主要讲element-wise add与concate的处理。下图以ResNet Block为例讲了不同的building block:
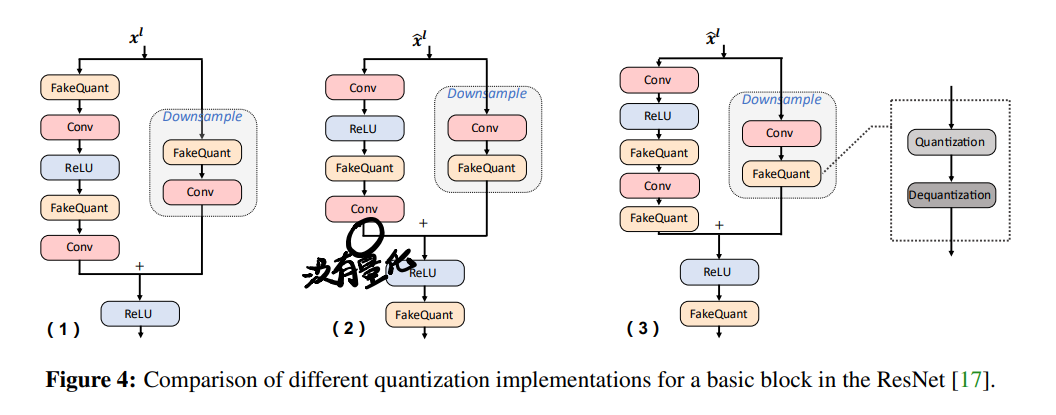
- 左图是academic implementation,块的输入(所以这会有啥问题?占用内存吗?)和elementwise-add都是在FP精度下操作的,这样会占用网络的throughput并影响latency(好的,问题解决),在某些结构中,受到I/O限制加速效果非常有限,另外downsample分支的activation需要单独量化,也会造成额外开销。
- 中图是TensorRT的实现方案。输入和输出被量化(实际上就是同一个地方吧,只是在两个块中),但是在elementwise-add中因为
the fusion with one of the former convolutional layer's bias addition所以以32-bit的形式进行; - 在FBGEMM这种其他的HW lib中要求element-wise add的所有输入都被量化,对于4-bit对称量化而言这会极大地损害性能。
4 MQBench Implementation
pytorch.fx的文档可能会有用。
5 MQBench Evaluation
评价的标准还挺合理的:
- test accuracy: academic setting下accuracy
- hardware gap:academic accuracy和deployment accuracy的区别
- hardware robustness:在5种架构下的accuracy平均值
- architecture robustness:不同架构下的accuracy(这个用平均排名不是更好?)
5.1 Evaluation with Academic Setting
所谓academic setting是指per-tensor、symmetric quantization、without BN folding的设置。
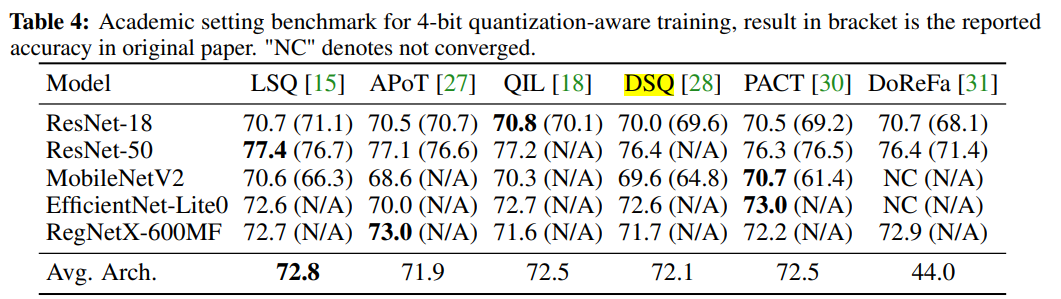
结论:
- 不同算法的差距没那么大(笑死,还diss了DSQ:相较DoReFa,80%的性能提升来自于训练技巧,只有两成来自算法);
- 没有哪个算法绝对最好/算法在结构间的鲁棒性挺差;
- rule-based algo能取得和learning-based algo相近的性能。
5.2 Evaluation with BN Folding
结论:
- BN folding对量化算法敏感,strategy 4总体上性能最好;
- strategy 4相比2/3加速也不明显;
- 更新batch statistics对BN fold的影响不大;
- data-parallel中BN statistics同步可以改善性能(但是花时间);
- lr warm-up可以解决BN folding导致初始阶段的不稳定性。
5.3 Evaluation with Graph Implementation
BN fold对量化算法敏感, 而图实现对网络结构敏感。
5.4 4-bit QAT
- test accuracy:还是不能分高下;不同hw与不同arch有不同的test accuracy方差,
depthwise conv-net(MobileNetV2 and EfficientNet-Lite) and per-tensor quantization (TVM and SNPE)的方差大; - Hardware Gaps:算法在academic setting与hardware setting间的差距都很大,没有哪个更好;
- Hardware & Architecture Robustness:网络结构对不同的量化算法敏感;hw robustness metric matters(比如LSQ在per-tensor情况下乱鲨,但是per-channel就拉了)。