DoReFa-Net: Training Low Bitwidth Convolutional Neural Networks with Low Bitwidth Gradients
2021/7/13
来源:arxiv16(最后是不投了吗,1.2k被引感觉好强!不愧是BNN经典作!)
resource:github上备份的包括ipad标注的pdf版本。
作者是旷视的Shuchang Zhou, Yuxin Wu, Zekun Ni, Xinyu Zhou, He Wen和Yuheng Zou,这篇文章也是BNN领域的开创性&代表性作品,但是很奇怪,这个组后面是金盆洗手了吗,怎么不见发其他BNN相关的文章了?
Summary:BNN领域非常具有代表性的作品,提出将模型的参数、激活值、梯度都进行量化(位数不定,根据需要调整),给出了敏感度梯度>激活值>参数的排名(因此需要的位数也是如此排序),因此加速在CPU, FPGA, ASIC和GPU等设备上的推理速度和训练速度(没想清楚,在FPGA上训练是怎么回事…真会有这样的需求吗?)。但是DoReFa给出的方案非常简单粗暴,所以影响也比较深?
rating:3.8/5.0
comprehension:4.0/5.0
文章的贡献有:
- 提出了同时量化模型权重、激活值和梯度的方法,指出参数、激活值、梯度的敏感程度依次上升,因此依次需要更多的位数;指出参数和激活值的量化是确定的,但是梯度的量化是随机量化;
- 提出merge activation和sign(这俩好像本来就是一回事233)的思路以减少中间结果和相应的内存消耗、中间计算,用查表(或类似,比较)的方式取值,应该启发了后面的boolnet?
2 DoReFa-Net
这里指出参数和激活值的量化是确定量化,梯度的量化是随机量化。
2.1 Using Bit Convolution Kernels in Low Bitwidth Neural Network
这节讲的是低比特乘法?对于两个定点数\(\Bbb{x}= \sum_{m=0}^{M-1}c_m(\Bbb{x})2^m\)和\(\Bbb{y}= \sum_{k=0}^{K-1}c_k(\Bbb{y})2^k\),那么\(\Bbb{x}\)和\(\Bbb{y}\)之间的点乘积可以用下式计算:\(\Bbb{x} \cdot \Bbb{y} = \sum_{m=0}^{M-1}\sum_{k=0}^{K-1}2^{m+k}bitcount[and(c_m(\Bbb{x}), c_k(\Bbb{y}))]\),计算的时间和\(\Bbb{x}\)与\(\Bbb{y}\)的位宽相关。
2.2 Straight Through Estimator
这里的forward形式(low-bit quantization)有点没见过:
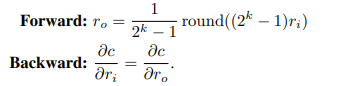
量化之后的比特串就按照上面的式子计算,再按情况scaling。
2.3 Low Bitwidth Quantization of Weights
- 细节:这里作者argue如果采用XNOR-Net中那种按通道scaling的方法会导致反向传播的时候计算梯度和权重之间的卷积不能充分开发bck(
However, the channel-wise scaling factors will make it impossible to exploit bit convolution kernels when computing the convolution between gradients and the weights during back propagation),所以本文对所有filter统一采用常数进行scaling(对所有权重都是如此):

在量化前使用tanh将范围限制到[-1, +1],式中的最大值是一层中所有权重的最大值(这里有点懵,这说明每层中参数必有能取到最大值的吗?)
2.4 Low Bitwidth Quantization of Activations
- 细节:作者在量化激活值前将它们通过了一个仿射层,将值范围映射成[0, 1]。
2.5 Low Bitwidth Quantization of Gradients
- 量化梯度的时候要引入随机性(是这个意思)
- 梯度取值范围变化可能比较大
- 细节:对梯度的量化有些特殊技巧:
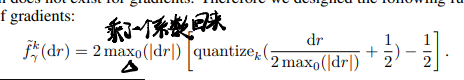
式中最大值是在除batch轴之外的轴上进行的(也就是每个batch会有一个最大值)。
需要引入一个随机噪声(作者声称这个对性能比较重要)\(N(k)=\frac{\sigma}{2^k-1}\),但是加的位置有点奇怪,直接塞到量化前的数值里去了(可以理解好吧,不然不就不是定点值了233):
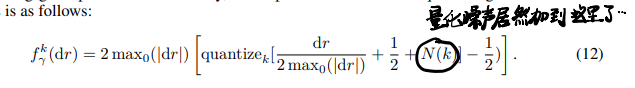
梯度的量化只在反传的时候进行(我寻思正向传播的时候也妹有啊…/有其他要量化的东西):
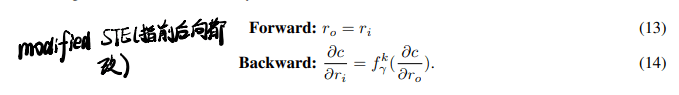
2.6 The Algorithm for DoReFa-Net
算法简单版如下所示:

2.7 First and The Last Layer
第一层最后一层不量化,但是最后一层的梯度有歧义,Nevertheless, the gradients back-propagated from the final FC layer are properly quantized.
2.8 Reducing Run-Time Memory Footprint By Fusing Nonlinear Function And Rounding
合并方法:
- merge step3、4、6(有点奇怪,step3也能合进来的吗?)
- 如果激活函数h是单调的,那么合成的f·h也是单调的,量化区间是一些不重叠的区域,可以用比较代替;
- merge step 11-13 ,如果中间有pooling那么情况会更复杂一些,但是如果是max pooling的话仍可用比较代替。
3 Experiments Results
3.1 Configuration Space Exploration
结论:
- 通道数更多对低比特量化越不敏感->增大通道数可以弥补量化。
- 对于通道数较少的模型,可以增大位宽来弥补性能。
- 梯度的最佳位宽和通道数目相关性较弱,在8-bit左右就实现了性能饱和。
3.2 Imagenet
结论:
- 保持参数1-bit,但是激活值从1-bit提到2-bit或4-bit能带来更高的性能提升(该发现早于binaryduo)。
- 在pretrained model和scratch model之间存在明显的性能gap(这个是我们想验证的结论?)
4 Discussion And Related Work
- 反传的时候需要计算全精度梯度和定点参数之间的卷积,所以反传效率还是低。
- 量化梯度的可能场景:在计算节点之间传量化梯度可以减少节点间通信量。