Learning Frequency Domain Approximation for Binary Neural Networks

2021/12/20

来源：NIPS21
resource：github上备份的包括ipad标注的pdf版本。
作者是华为诺亚的Yixing Xu, Kai Han, Chang Xu, Yehui Tang, Chunjing Xu, Yunhe Wang，水平只能算还行。

Summary：一篇中规中矩的BNN文章，文章的出发点是现在的STE近似方法破坏了实际梯度的主要方向（文章没展开讲，我理解是说一般的STE近似都是用形状相似的函数代替，而他们的这个把sgn拆解成高低频分量，又保留了主要的低频部分，所以保护了主要方向？有点牵强），为此他们做了两个事情，①将sgn拆成傅里叶级数，反传的时候用低频分量的组合近似梯度②为了避免级数n过大导致训练不稳定、开销大，他们对每个W/A补了一个noise adaptation module来弥补高频部分缺失造成的表示误差。

rating：3.5/5.0
comprehension：4.5/5.0

文章的贡献有：

• 提出将sgn拆成傅里叶级数，作为反传时梯度的近似，以改进STE；
• 一种module design，用来弥补高频分量丢失造成的误差。

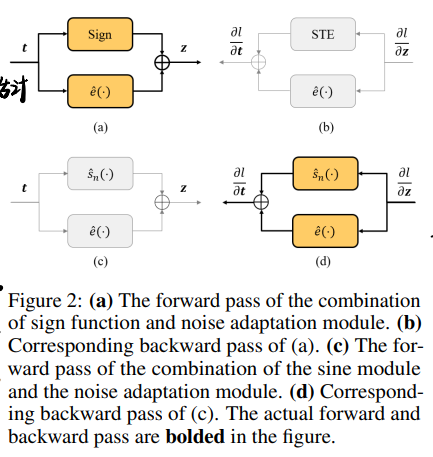
一张图总结本文流程：

2 Approach

提了一个新概念，有点受用，zero-order (derivative-free) algorithms - 0阶优化，比如进化算法；first-order optimization algorithms - 1阶优化，比如SGD。

2.2 Decomposing Sign with Fourier Series

简直就像回到了娘家，这里把sgn函数拆成了傅里叶级数，也是本文最主要的贡献：

2.3 Solving the Inaccurate Estimation Problem

将sgn函数和拟合函数之间的误差作为噪声，添加noise adaptation module来稳定训练，对$r(t)$的分布有一些限制（0均值，有限方差），并且认为模块的输入满足正态分布，因此NAM的初始化也有一些相应的限制，有点牵强.

具体而言，NAM是两个FC层再加一个跳连：

sine module只在反传中用到，而且误差估计项随着训练逐渐变成0，具体可以参考一图总结。

本文的算法如下所示：

这里第三行有点问题，训练中前传的时候并不是真二值，直到训练结束的时候NAM的作用才被取消，原文为证：

In order to keep the weights and activations as 1-bit in inference, the sine module is used only in 
the backward pass and replaced as sign function in the forward pass, ... Besides, alpha is gradually
decreased during training and reaches 0 at the end of training to avoid the inconsistency between
training phase and inference phase

• 所以正确的流程应该是，前传sgn + NAM，反传sine + NAM，训练结束NAM anneal到0，推理时前传用sgn。

3 Experiments

CIFAR10上的结果：

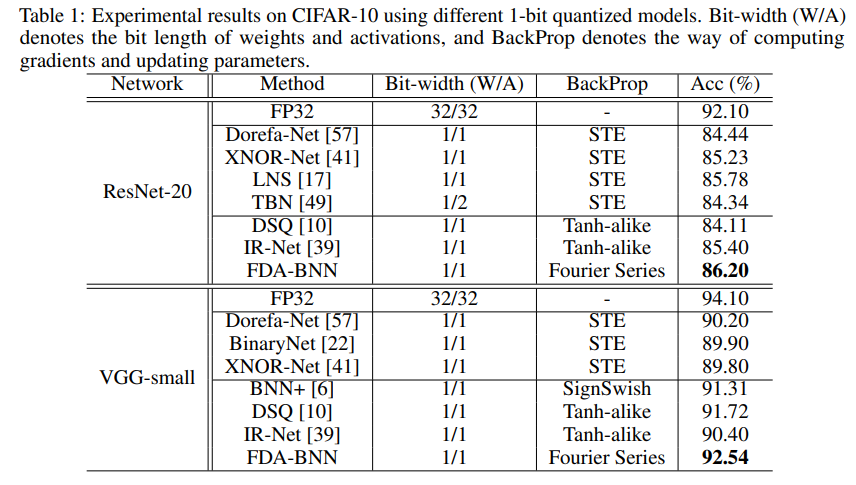
ImgNet上的结果：