Automated Log-Scale Quantization for Low-Cost Deep Neural Networks
2021/8/28
来源:CVPR2021 resource:github上备份的包括ipad标注的pdf版本。
作者是韩国国立蔚山科学技术院的Sangyun Oh, Hyeonuk Sim, Sugil Lee和Jongeun Lee。
Summary:传统的对数量化方案在位宽比较宽裕的情况下相比均匀量化产生的量化误差更大,因此有了一种selective two-word logarithmic quantization(STLQ)的量化方案,大意是当对数量化的量化误差大于一个门槛的时候,对残差再进行一次对数量化。这种选择性两字对数量化对应的量化训练开发得还不是很充分,所以作者提出了一种基于STLQ的训练方案。具体而言,作者将参数分成了两组,一组是1word对数量化,另一组是2-word对数量化,两组参数分开训练,中间用两种tensor C和v进行了联系,其他的改进还有改变了分组粒度,从一般的按filter改成了按tile。虽然好像不是很难的东西,但是最后结果还挺不错的,在SID Dataset上用W3A6(只有W是STLQ,A是linear)上取得了27.78PSNR的性能(15% 2-word)。
Rating: 3.5/5.0
Comprehension: 3.5/5.0
大概可用一张图描述他们的量化方案:
1 Introdution
- 非均匀量化相比均匀量化的优点,在硬件实现上更简单,按照量化是对W还是对W/A都进行可以把乘法器改成移位器或者加法器(未深究);
- 当大幅值的参数对精度有显著影响时,在位宽相等的情况下,对数量化要比均匀量化效果差(讲道理这段写得真差):
This can sometimes lead to a lower expected quantization error overall, but often disproportionately high error
that happens at high-magnitude values can undermine the accuracy of a log-scale quantization scheme significantly,
resulting in worse performance than linear quantization at the same bit-width
-
STLQ的硬件实现难度和对数量化一样,性能接近均匀量化。
-
抨击了以前基于STLQ的训练方案(感觉大多不make sense):
- 说2-word比例是个超参数,在同一层或同一通道固定,或者不好优化 —— (这不是粒度的问题吗,有必要这么讲吗?
- 之前的工作的优化目标是量化误差,而不是用潜变量显式地约束模型size和2-word比例,因此训练不是最优的 —— ??你开心就好…这不该给个ablation吗?
- 不能在给定ratio下找到最佳参数 —— …
3 Preliminaries on Log-Scale Quantization
对于对数量化和STLQ的描述还是有用的:
3.1 Preliminaries on Log-Scale Quantization
对于来自范围[-1, +1]的x,将其量化为一个N-bit的整数q,q的范围是[-M, M-1],其中\(M=2^{N-1}\),重建的\(\tilde{x}\)可以表示为:
\[LogDequant : \tilde{x} = \begin{cases} &0 \quad &if \quad q = 0 \\ &sign(q)2^{-|q|} \quad &otherwise. \end{cases}\]对应的对数量化器为:
\[Logquant : q = \begin{cases} &clip\left( - \lfloor log_2(\frac{|x|}{U}) \rceil, 1, M-1\right) \quad &if \quad x>0 \\ &0 \quad &if \quad x = 0 \\ &-clip\left( - \lfloor log_2(\frac{|x|}{U}) \rceil, 1, M\right) \quad &otherwise. \end{cases}\]式中的clip函数定义为\(clip(x,a,b) = min(max(x,a),b)\),\(\lfloor \rceil\)表示round函数,U是个scaling factor(比如\(\begin{vmatrix}x\end{vmatrix}\)的最大值)。下式表示从x到\(\tilde{x}\)的变换:
\[LogQ : x → \tilde{x} = LogDequant \circ LogQuant\]Selective Two-word Logarithmic Quantization
这里介绍了STLQ,先给个流程图会比较好:
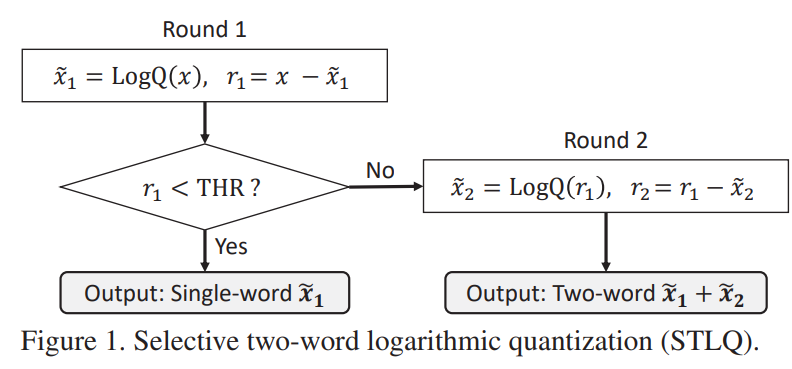
Round1:
\[\tilde{x_1} = LogQ(x), \quad \quad r_1 = x - \tilde{x_1}\]Round2:
\[\tilde{x_2} = LogQ(r_1), \quad \quad r_2 = r_1 - \tilde{x_2}\]选择1-w或者2-w的粒度叫做quantization cardinality granularity,如果这个粒度是filter的话,那么整个filter中的平均量化误差\(\begin{Vmatrix}\mathbf{r_1}\end{Vmatrix}_2\)将会拿去和threshold比。
4 Our Proposed Training Method
4.1 Our Proposed Training Method
这里讲他们的idea有两条:
- 将weight分成两簇,一簇专门用来减少task loss而不考虑residual(也就是2-word),另一簇专注于减少量化误差。
- auxiliary tensor v,这里没介绍,实际上是软化的flag,表示weight分类。
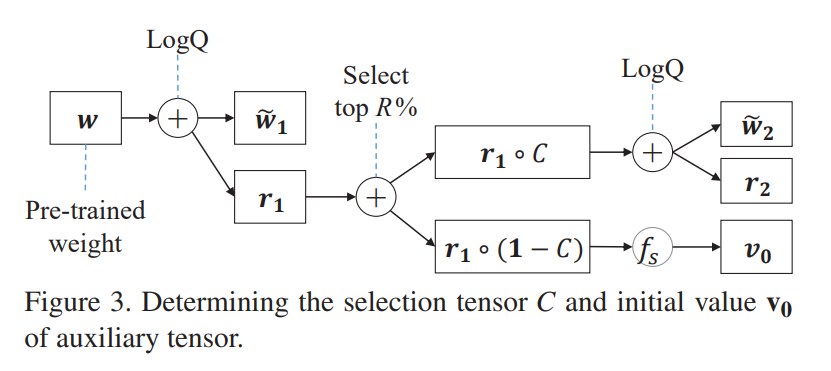
下面这张图给了他们的训练流程:

本质上还是finetune,对w没有太大变化(也就是为什么下文讲C一旦确定不会变化)
4.2 Selection Tensor
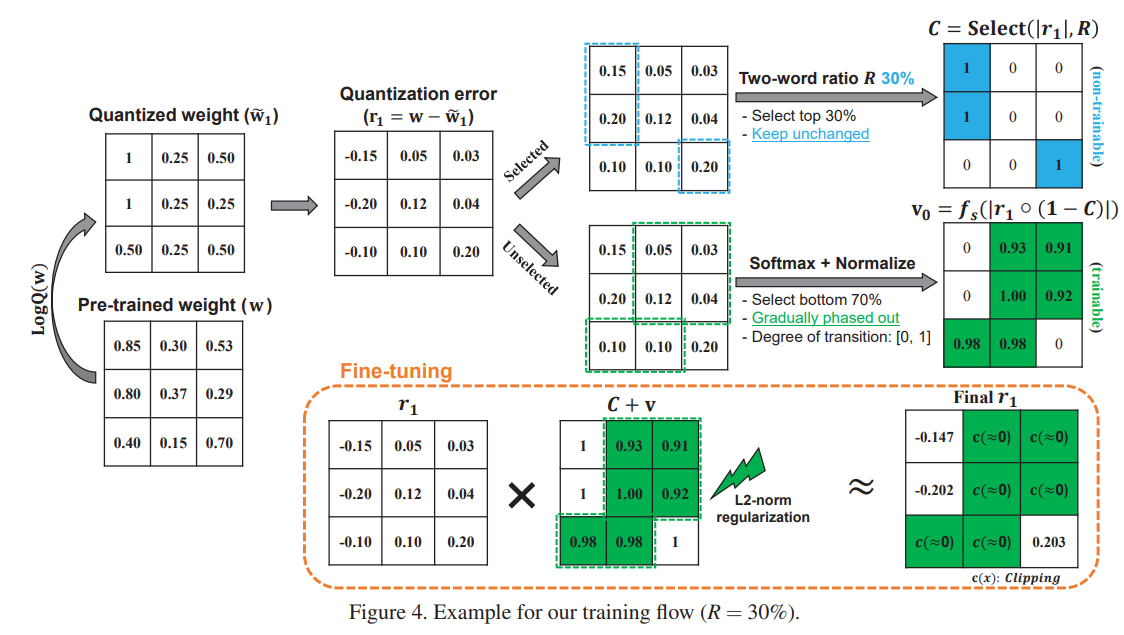
一张图就能说清楚这个tensor是怎么回事:
C是个binary tensor,是区分selected weight和unselected weight的硬标签,一旦确定就不再变化。图里面的\(f_s\)和\(v_0\)后面会介绍。
4.3 Fine-tuning and Initializing Auxiliary Tensor
这个方法是在finetune过程中逐渐取消未被选择的参数的2-word效果,做法是在\(r_1\)上乘个系数,这个系数由C和v构成,在训练中逐渐把v anneal到0,为此设计的loss为:
\[l(\mathbf w, \mathbf v)=l_{task}(\tilde{\mathbf w}) + \lambda ||\mathbf v||^2_2 \\ \tilde{\mathbf w} = \tilde{\mathbf w_1} +LogQ(\mathbf r_1 \circ (C + \mathbf v))\]v和C互补,在训练中逐渐anneal到0,低于一个门槛直接truncate到0。用softmax和最大值归一化来初始化\(v_1\):
\[\mathbf v_0 = f_s (|\mathbf r_1 \circ (\mathbb 1 - C)|) \\ f_s(\mathbf x) = normalize(softmax(\mathbf x))\]4.4 Per-Tile Quantization
tile的本质是给不同的weight分组(不同字长的weight混在一起会降低整体速度,不难理解),分组相同的weight的字长粒度一样,有一张诡异的图应该可以说明问题:
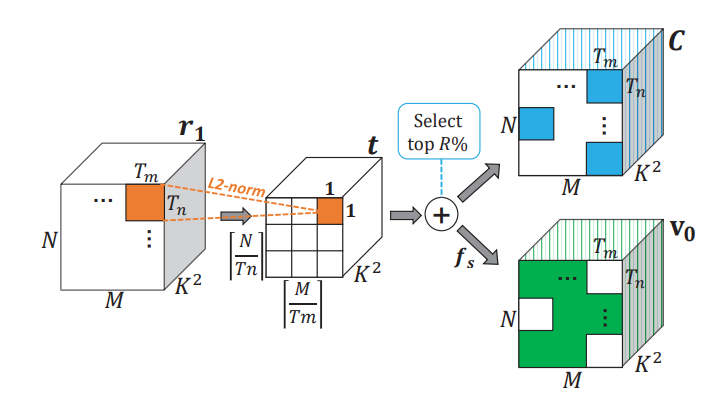
4.5 Discussion: Differences from Previous Work
作者argue自己的创新点:
- 其他工作是整体往1-w优化,但是本文是只优化没被选中的参数,另外的参数用2-w,不变。
- 与直接减少\(r_1\)不同,作者引入了一个tensor v,同时优化tensor v 和 w(但是这个和上一条不是紧密相关的吗?)。
- per-tile scheme。
5 Experimental Setup
- 图像增强和语义分割任务需要更高的activation精度。
- light-weight的模型也需要更高的act精度。
- 他们的结果: