2021/6/3结果反馈与讨论记录

2021/6/1

CDG效果验证

CDG_ResNet实现方案

# CDG v2 / cleaned CDG
# This is an updated version of CDG calculating on ResNet
# input: model - the model to calculate CDG grad
#        epsilon - the hyperparameter of CDG
#        name - specify some layers to compute CDG
#        
def calc_CDG(model, inputs, target, epsilon=1e-1, name=None, device='cuda'):
    original_weights = copy.deepcopy({n:v.clone() for n,v in model.state_dict().items()})
    shape = original_weights[name].shape
    CDG_grad = torch.zeros(shape)
    time_start = time.time()
    for i in range(shape[0]):
        for j in range(shape[1]):
            for k in range(shape[2]):
                for m in range(shape[3]):
                    original_weights[name][i][j][k][m] += epsilon
                    model.load_state_dict(original_weights)
                    logits = model(inputs)
                    loss_p = trainer._obj_loss(inputs, logits, target, model,
                                      add_evaluator_regularization=trainer.add_regularization)
                    original_weights[name][i][j][k][m] -= 2*epsilon
                    model.load_state_dict(original_weights)
                    logits = model(inputs)
                    loss_m = trainer._obj_loss(inputs, logits, target, model,
                                      add_evaluator_regularization=trainer.add_regularization)
                    original_weights[name][i][j][k][m] += epsilon
                    CDG_grad[i][j][k][m] = (loss_p.item()-loss_m.item()) / (2 * epsilon)
    time_end = time.time()
    print("consuming time {}s".format(time_end - time_start))
    return CDG_grad

Rosenbrock函数上测试CDG

实验条件：

• 在Rosenbrock函数上测试CDG，采用下图红框所示的形式（简单Rosenbrock函数，50对非耦合变量）：

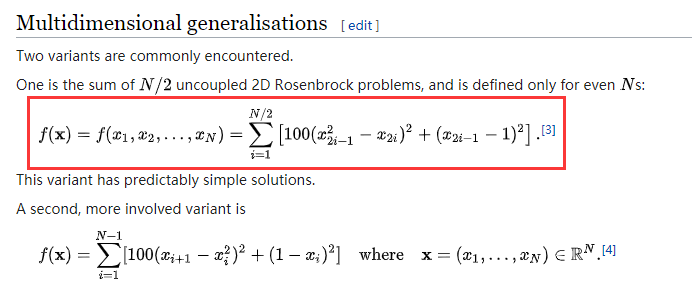
• 参数设置如下：
  • Rosenbrock参数：N=100, a=1, b=100, x为dim=100且初始值在[-10, 10]上均匀分布的随机整数；
  • CDG参数：初始lr=1e-1, epsilon=1e-2, 在30k更新后每隔10k对lr和epsilon乘以系数0.1。

实验结果：

• 初始值/更新前期：

• 更新中期/改变lr&epsilon前后：

• • 改变lr/epsilon前rosenbrock value陷入了局部最优，不再下降
  • 改变lr/epsilon前x的值就已经非常接近全局最优值(all ones)了
  • 改变lr/epsilon后rosenbrock value发生很大改善
• 更新末期：

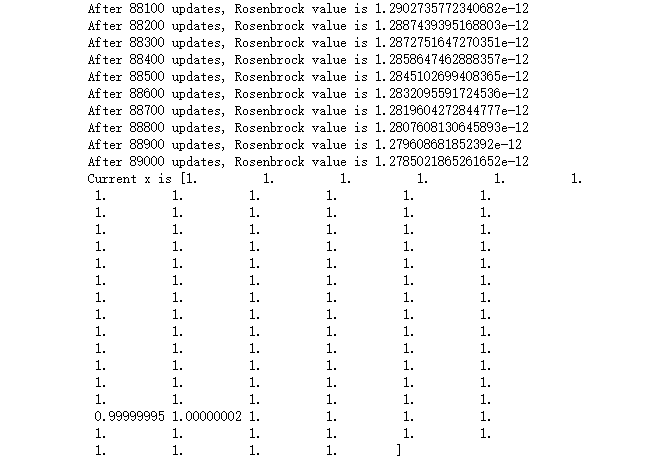
• • 可以认为x收敛到了全局最优值。

一些讨论：

• CDG在rosenbrock这种简单的全精度函数上是有效的；
• CDG效果不佳的原因（比如陷入局部最优）可能是epsilon/lr取值不当造成的（binary model上的困难？）。

Discrete Gradient测试

实验算法：https://www.overleaf.com/9353518124fvqvqdhwkdwf
实现方案：

• 对于给定的$\epsilon$和$\delta_d$的搜索步长stride，对于所有的维度进行以下搜索：
  • （每一维的搜索）当前$\delta_d=stride*(i+1)$，其中$i$是循环计数，对该维度参数增减$\delta_d$直到出现$f decrease$或$\delta_d$达到上限（$\epsilon$），记录该维最小$\delta_d$与对应的$f decrease$；
  • 搜索每一维的$\delta_d$后按照algo中分式计算$objective$，按照大小对$objective$排序并由大到小将$objective$对应的$\delta_d$写入向量DG（即取为最终更新的维度），重复该选择过程直到$\sum_{d=1}^D \delta_d^2 < \epsilon^2$的条件不再满足。

实验结果：

• epsilon=1e-1, search_stride=1e-4的情形(quick check, delta_d distribution)：

• epsilon=1e-2, search_stride=1e-5的情形(quick check, delta_d distribution)：

一些讨论：

*stochastic rounding STE实验补充

实验条件：

• 在三层32neuron-MLP上测试，预训练（如有）采用 bs = 16000 的 batch（数据i.i.d.采样自N(0, 1)）训练 500 step至 loss 收敛；
• FP weight & Binary activation；
• stochastic rounding STE修改成，在更新前后inference时采用普通的sign函数，在更新阶段的inference采用sr-STE（相当于为普通的STE引入一定随机性）
• 后续STE/sr-STE梯度下降时 bs=1024 (在10个不同的batch上分别测试，以期消除部分随机性)，lr在从 1e-5 开始，以 1e-5 为间隔，至 0.5 的区间上扫描，取使得loss最小的值；
• sr-STE grad的计算方式是，inference时对activation的量化采用stochastic rounding，计算出带有扰动的grad，将N次采样（1-10次采样）得到的grad累加起来取平均并normalize。

*Updated sr-STE on raw model

log可参考这个txt文件。
下面的曲线都是更新前后的loss值，该值越小越好。

• 情形一(sr-STE随采样次数增多效果逐渐变差)：

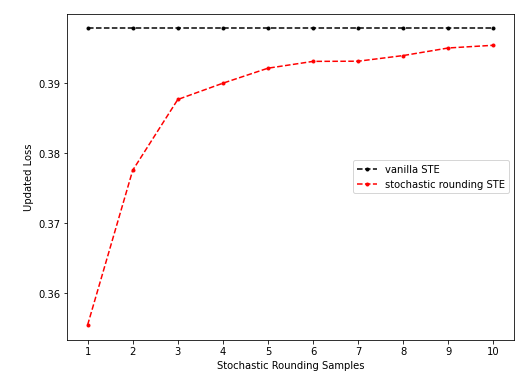
上图是未预训练的、固定sr-STE（只在计算grad时取sr）、第一个batch上的结果，表现出了sr-STE updated loss随着采样数增加也逐渐增加的特性。

• 情形二(sr-STE随采样次数增多效果振荡)：

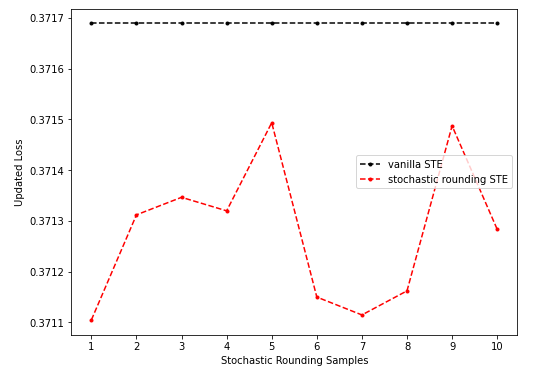
上图是未预训练的、固定sr-STE（只在计算grad时取sr）、第四个batch上的结果，采样次数增加并不会一致地使loss改善，而是出现了振荡。

• 情形三(sr-STE随采样次数增多效果逐渐变好)：

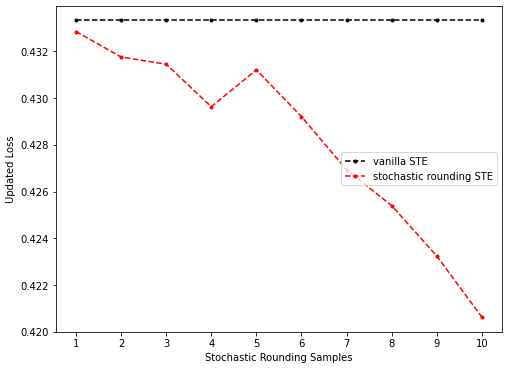
上图是未预训练的、固定sr-STE（只在计算grad时取sr）、第二个batch上的结果，随着采样次数增多，loss逐渐下降。

一些讨论：

• 在训练初期使用Fixed sr-STE总可以使loss下降(相比原始loss)，而且在10个测试的batch上，Fixed sr-STE的更新结果总要优于vanilla STE（有点奇怪，这可能是初始化、样本随机性造成的，且不清楚在真实模型上是否有此表现）；
• 增加采样数不会出现loss一致改善的情况，这应该是sr随机性造成的 -> 不同的采样应根据其效果有不同的重要性/加权系数，而不是均匀加权。

*Updated sr-STE on pretrained model

log可参考这个txt文件。
下面的曲线都是更新前后的loss值，该值越小越好。

• 情形一（sr-STE的结果和vanilla STE接近）：

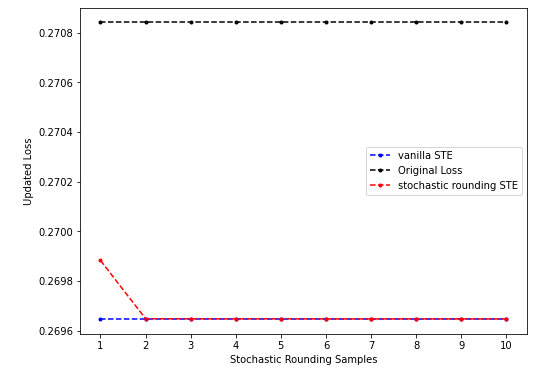
上图是预训练的、固定sr-STE（只在计算grad时取sr）、第一个batch上的结果，vanilla STE和sr-STE都能产生梯度下降，当MC sample上升的时候sr-STE的效果(0.2696472704410553)可以非常接近vanilla-STE(0.26964688301086426)。

• 情形二（sr-STE的结果差于vanilla STE）：

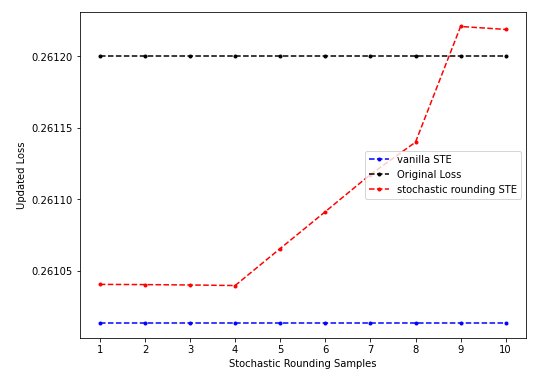
上图是预训练的、固定sr-STE（只在计算grad时取sr）、第二个batch上的结果，sr-STE随着sample数目增多反而会恶化最后甚至不如原始loss的情形。

• 情形三（sr-STE的结果优于vanilla STE）：

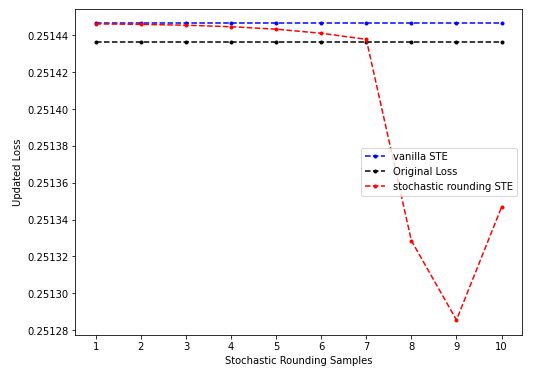
上图是预训练的、固定sr-STE（只在计算grad时取sr）、第三个batch上的结果，sr-STE随着sample数目增多效果渐好最后优于原始loss的情形。

在10个batch上得到的一些统计数字：

• 不同MC sample数下sr-STE更新优于vanilla STE（只要某一sample数下sr-STE优于vanilla STE即计入），频次8/10；
• vanilla STE可以使loss下降(7/10)；
• sr-STE更新后loss始终低于原始loss(8/10)；随sample数增多，sr-STE更新后loss由低于原始loss变为高于原始loss(1/10)；随sample数增多，sr-STE更新后loss由高于原始loss变为低于原始loss(1/10)。

一些讨论：

• 引入随机性的STE在训练末期有较高的概率仍能找到loss下降的方向，且在大部分时候表现要优于vanilla STE（指loss下降更多，但这可能是： ①batch数较少导致的随机性 ②模型过于简单，在真实模型上不适用 导致的）；
• 在一个batch上可以产生更好的loss下降，是不是lr sweeping带来的增益？在一个batch上sr-STE优于STE（如是）在全局的更新上会有何种表现？真实模型上又会有怎样的表现？

会议讨论

• 陈老师：
  • 在backward阶段引入随机性？多个方向，含有下降的方向。
  • NES在高维情况下不是很适合：sample complexity -> sample proposal